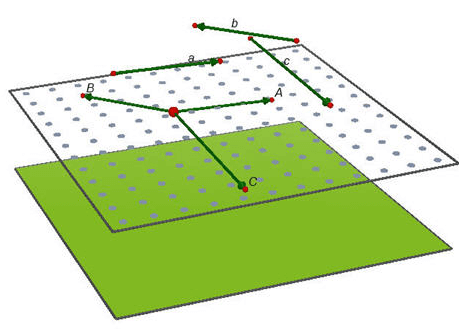
Trong không gian cho ba vectơ tùy ý \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\)
Gọi \(\overrightarrow{u}=\overrightarrow{a}-2\overrightarrow{b};\overrightarrow{v}=3\overrightarrow{b}-\overrightarrow{c};\overrightarrow{w}=2\overrightarrow{c}-3\overrightarrow{a}\)
Chứng tỏ rằng ba vectơ \(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\) đồng phẳng ?