Trên mặt phẳng Oxy hãy tính góc giữa hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) trong các trường hợp sau :
a) \(\overrightarrow{a}=\left(2;3\right);\overrightarrow{b}=\left(6;4\right)\)
b) \(\overrightarrow{a}=\left(3;2\right);\overrightarrow{b}=\left(5;-1\right)\)
c) \(\overrightarrow{a}=\left(-2;-2\sqrt{3}\right);\overrightarrow{b}=\left(3;\sqrt{3}\right)\)

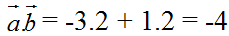
a) cos(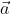 ;
; 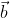 ) =
) =  = 0
= 0
=> (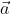 ;
; 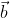 ) = 900
) = 900
b) cos(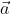 ;
; 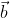 ) =
) =  =
= 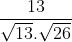
=> (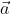 ;
; 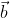 ) = 450
) = 450
c) cos(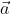 ;
; 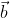 ) =
) =  =
= 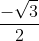
=> (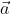 ;
; 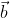 ) = 1500
) = 1500
Đăng những câu khác đi em mỏi tay rồi
kéo thả chuột mà cũng kêu mỏi ?