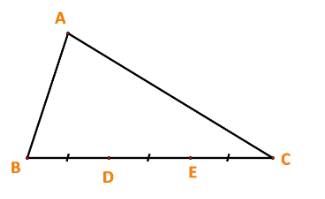
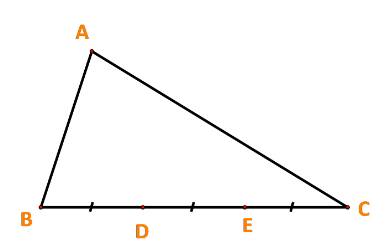
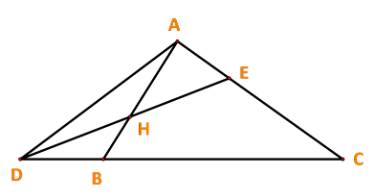
a) Cho tam giác ABC. Gọi D, E lần lượt là các điểm thỏa mãn: \(\overrightarrow{BD}=\dfrac{2}{3}\overrightarrow{BC};\overrightarrow{AE}=\dfrac{1}{4}\overrightarrow{AC}.\)Tìm vị trí của điểm K trên AD sao cho 3 điểm B, K, E thằng hàng.
b) Cho tam giác ABC vuông tại A; BC = a; CA = b; AB = c. Xác định điểm I thỏa mãn hệ thức: \(\left(b^2MB^2+c^2MC^2-2a^2MA^2\right)\) đạt giá trị lớn nhất.


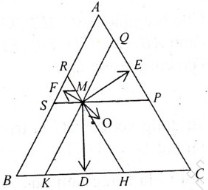
 B1C2 nên MD cũng là trung điểm thuộc cạnh B1C2 của tam giác MB1C2
B1C2 nên MD cũng là trung điểm thuộc cạnh B1C2 của tam giác MB1C2 =
= 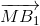 +
+ 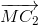
 =
= 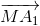 +
+ 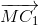
 =
= 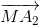 +
+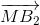
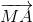
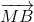
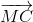
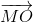 .
.