Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 : Bài giải
Ta có : \(\widehat{A}-\widehat{B}=10^o\text{ }\Rightarrow\text{ }\widehat{A}=\widehat{B}+10^o\)
Trong tứ giác ABCD có :
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\widehat{B}+10+\widehat{B}+60^o+80^o=360^o\)
\(2\widehat{B}+150^o=360^o\)
\(2\widehat{B}=110^o\)
\(\widehat{B}=55^o\text{ }\Rightarrow\text{ }\widehat{A}=65^o\)

a) Ta thấy : A + B + C + D = 360°
Tự áp dụng tính chất dãy tỉ số bằng nhau ta có :
A = 144°
B = 108°
C = 72°
D = 36°
b) Vì DE , CE là phân giác ADC và ACD
=> EDC = ADE = 18°
=> BCE = ECD = 36°
Xét ∆DEC ta có :
EDC + DEC + ECD = 180°
=> DEC = 126°
Ta có : góc ngoài tại đỉnh C
=> 180° - BCD = 108°
Góc ngoài tại đỉnh D
=> 180° - ADC = 144°
Mà DF , CF là phân giác ngoài góc C , D
=> CDF = 72°
=> DCF = 54°
Xét ∆CDF ta có :
CDF + DFC + DCF = 180°
=> DFC = 44°

a: Xét tứ giác ABCD có
\(\widehat{BAD}+\widehat{ADC}+\widehat{ABC}+\widehat{BCD}=360^0\)
\(\Leftrightarrow2\cdot\left(\widehat{DAH}+\widehat{HDA}\right)=180^0\)
\(\Leftrightarrow\widehat{HAD}+\widehat{HDA}=90^0\)
\(\Leftrightarrow\widehat{AHD}=90^0\)

a) Sử dụng tính chất dãy tỉ số bằng nhau. A ^ = 144 0 , B ^ = 108 0 , C ^ = 72 0 , D ^ = 36 0
b) Sử dụng tổng ba góc trong tam giác tính được C E D ^ = 126 0 .
Chú ý hai phân giác trong và ngoài tại mỗi góc của một tam giác thì vuông góc nhau, cùng với tổng bốn góc trong tứ giác, ta tính được C F D ^ = 54 0
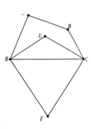

1. Áp dụng định lý tổng 3 góc vào tam giác ICD , bạn tính được góc ICD +góc IDC = 75 độ
Mà góc BCD = 2 góc ICD và góc ADC = 2 góc IDC nên góc BCD + góc ADC = 2.75 = 150 độ
Xét tứ giác ABCD có: góc A + góc B + góc BCD + góc ADC = 360 độ
góc A + 90 độ + 150 độ = 360 độ
góc A = 120 độ
2. góc C của tứ giác là: 180 độ -130 độ = 50 độ
Chúc bạn học tốt.

Bạn tham khảo tại đây:
Bài 8 Sách bài tập - trang 80 - Toán lớp 8 | Học trực tuyến
Bạn chú ý cái đường link rồi sửa thành h là OK hết chỗ nói nha.Hoặc là ib với mik rồi mik cho:3
Xét tứ giác ABCD có \(\widehat{BAD}+\widehat{ABC}+\widehat{BCD}+\widehat{ADC}=360^0\)
=>\(\widehat{BCD}+\widehat{ADC}=360^0-220^0=140^0\)
\(\widehat{KDC}+\widehat{KCD}=\dfrac{180^0-\widehat{BCD}}{2}+\dfrac{180^0-\widehat{ADC}}{2}\)
\(=\dfrac{360^0-140^0}{2}=110^0\)
Xét ΔKCD có \(\widehat{KDC}+\widehat{KCD}+\widehat{CKD}=180^0\)
=>\(\widehat{CKD}+110^0=180^0\)
=>\(\widehat{CKD}=70^0\)