
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi AH là cc tương ứng với BC
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\)

Nối \(AE\), tam giác \(EAC\) có chiều cao bằng độ dài đoạn \(AD=10cm\).
Diện tích tam giác \(EAC\) bằng:
\(\frac{50\times10}{2}=250\left(cm^2\right)\)
Diện tích tam giác \(ABC\) bằng:
\(\frac{50\times40}{2}=1000\left(cm^2\right)\)
Diện tích tam giác \(BAE\) ( bằng diện tích tam giác \(ABC\) trừ đi diện tích tam giác \(EAC\) ):
\(1000-250=750\left(cm^2\right)\)
Chiều cao \(ED\) của tam giác \(BAE\) bằng:
\(\frac{750\times2}{40}=37,5\left(cm\right)\)
Độ dài cạnh \(BC\) bằng:
\(50-10=40\left(cm\right)\)
Vì \(DE\) song song với \(AC\) nên \(DE\) vuông góc với \(BD\). Vậy tam giác \(BDE\) là tam giác vuông tại \(D\) và có diện tích bằng:
\(\frac{40\times37,5}{2}=750\left(cm^2\right)\)
Đáp số: \(750cm^2\)
\(S\) \(ABC:\frac{40\times50}{2}=1000\left(cm^2\right)\)
\(S\) \(AEC:\frac{50\times10}{2}=250\left(cm^2\right)\)
\(S\) \(ABE:1000-250=750\left(cm^2\right)\)
\(DE:\frac{750\times2}{40}=37,5\left(cm\right)\)
\(S\) \(BDE:\frac{37,5\times30}{2}=562,5\left(cm^2\right)\)

it's so easy, I didn't expect you could not answer this question, what a lousy

MDAC là hình thang có chiều cao 10cm
=>MD//AC và AD=10cm
DB+AD=AB
=>DB+10=30
=>DB=20(cm)
Xét ΔBAC có MD//AC
nên \(\dfrac{MD}{AC}=\dfrac{BD}{BA}\)
=>\(\dfrac{MD}{60}=\dfrac{20}{30}=\dfrac{2}{3}\)
=>\(MD=60\cdot\dfrac{2}{3}=40\left(cm\right)\)
Diện tích hình thang ADMC là:
\(S_{ADMC}=\dfrac{1}{2}\cdot AD\cdot\left(MD+AC\right)\)
\(=\dfrac{1}{2}\cdot10\cdot\left(60+40\right)=5\cdot100=500\left(cm^2\right)\)
Diện tích tam giác ABC là:
\(S_{ACB}=\dfrac{1}{2}\cdot AB\cdot AC=900\left(cm^2\right)\)
\(S_{ABC}=S_{BMD}+S_{CMDA}\)
=>\(S_{BMD}+500=900\)
=>\(S_{DMB}=400\left(cm^2\right)\)
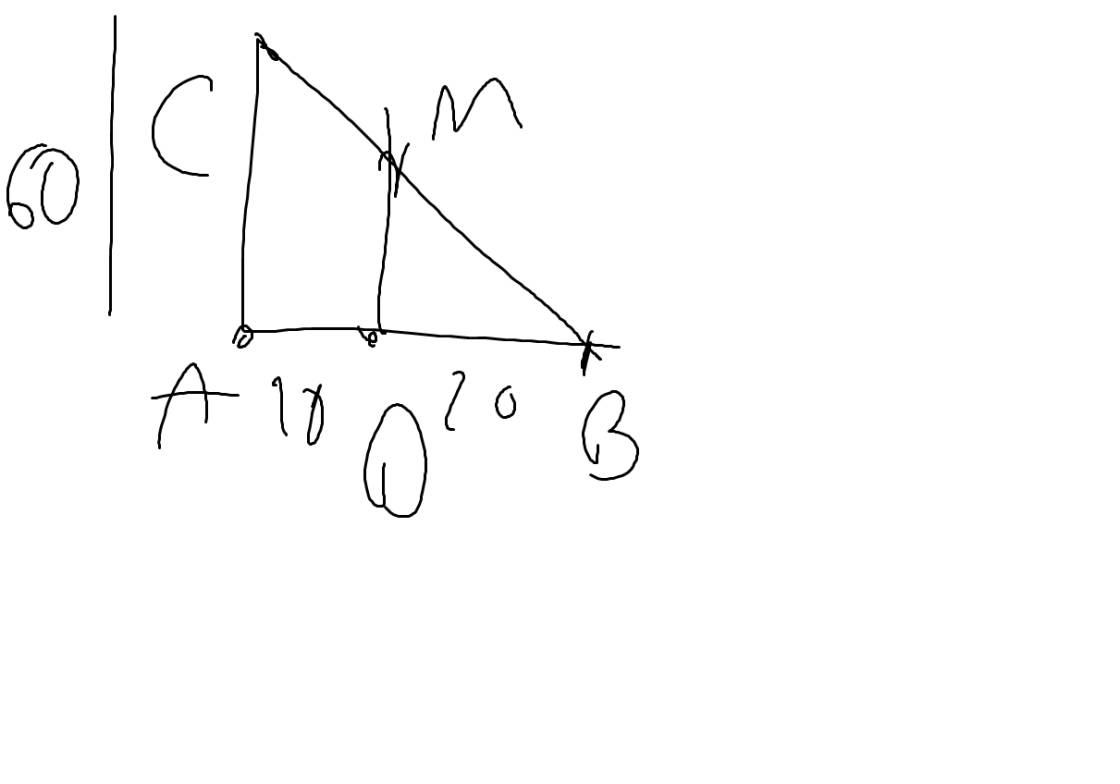
D bạn nhé
D hoặc A bạn nhé
Vì ở đây nếu AC = 10 cm thì BC = 10 cm ( Đúng )
Hoặc AC = 5 cm thì BC = 15 cm ( Đúng )
Nên nếu đề ch ABC là tam giác cân thì Ac bằng 10 cm còn nếu cho thêm dữ kiện BC = 15 cm thì AC = 5 cm nhé