K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HA
3
25 tháng 7 2023
\(x^2-5x+6=\left(x-2\right)\left(x-3\right)\)
\(x^2-7x+12=\left(x-2\right)\left(x-5\right)\)
\(x^2+x-12=\left(x-5\right)\left(x+6\right)\)
\(x^2-9x+20=\left(x-4\right)\left(x-5\right)\)
QA
5 tháng 8 2021
Trả lời:
7, 5( x + y )2 + 15( x + y )
= 5( x + y )( x + y + 3 )
9, 7x( y - 4 )2 - ( 4 - y )3
= 7x ( 4 - y )2 - ( 4 - y )
= ( 4 - y )2 ( 7x - 4 + y )
11, ( x + 1 )( y - 2 ) - ( 2 - y )2
= ( x + 1 )( y - 2 ) - ( y - 2 )2
= ( y - 2 )( x + 1 - y + 2 )
= ( y - 2 )( x - y + 3 )
8, 9x ( x - y ) - 10 ( y - x )2
= 9x ( x - y ) - 10 ( x - y )2
= ( x - y )[ ( 9x - 10 ( x - y ) ]
= ( x - y )( 9x - 10x + 10y )
= ( x - y )( 10y - x )
10, ( a - b )2 - ( a + b )( b - a )
= ( b - a )2 - ( a + b )( b - a )
= ( b - a )( b - a - a - b )
= - 2a( b - a )
= 2a ( a - b )
12, 2x ( x - 3 ) + y ( x - 3 ) + ( 3 - x )
= 2x ( x - 3 ) + y ( x - 3 ) - ( x - 3 )
= ( x - 3 )( 2x + y - 1 )
CD
2
2 tháng 9 2021
a: \(\dfrac{x^2-5x+6}{x^2+7x+12}:\dfrac{x^2-4x+4}{x^2+3x}\)
\(=\dfrac{\left(x-2\right)\left(x-3\right)}{\left(x+3\right)\left(x+4\right)}\cdot\dfrac{x\left(x+3\right)}{\left(x-2\right)^2}\)
\(=\dfrac{x\left(x-3\right)}{\left(x-2\right)\left(x+4\right)}\)
2 tháng 9 2021
b: \(\dfrac{x^2+2x-3}{x^2+3x-10}:\dfrac{x^2+7x+12}{x^2-9x+14}\)
\(=\dfrac{\left(x+3\right)\left(x-1\right)}{\left(x+5\right)\left(x-2\right)}\cdot\dfrac{\left(x-2\right)\left(x-7\right)}{\left(x+3\right)\left(x+4\right)}\)
\(=\dfrac{\left(x-1\right)\left(x-7\right)}{\left(x+5\right)\left(x+4\right)}\)
CM
19 tháng 1 2017
a) (x - 2)(x - 3). b) 3(x - 2)(x + 5).
c) (x - 2)(3x + 1). d) (x-2y)(x - 5y).
e) (x + l)(x + 2)(x - 3). g) (x-1)(x + 3)( x 2 + 3).
h) (x + y - 3)(x - y + 1).
CM
22 tháng 10 2017
1 x . x x + 1 . x + 1 x + 2 . x + 2 x + 3 . x + 3 x + 4 . x + 4 x + 5 . x + 5 x + 6 . x + 6 x + 7 . x + 7 x + 8 . x + 8 x + 9 . x + 9 x + 10 . x + 10 1 = 1
HT
3
26 tháng 7 2021
a, \(x^2-5x+6=x^2+x-6x+6=x\left(x-1\right)-6\left(x-1\right)=\left(x-1\right)\left(x-6\right)\)
b, \(3x^2+9x-30=3\left(x^2+3x-10\right)=3\left(x^2-2x+5x-10\right)\)
\(=3\left[x\left(x-2\right)+5\left(x-2\right)\right]=3\left(x-2\right)\left(x+5\right)\)
c, \(x^2+7x+10=x^2+2x+5x+10=x\left(x+2\right)+5\left(x+2\right)=\left(x+2\right)\left(x+5\right)\)
TN
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1
\(\Leftrightarrow x+\dfrac{1}{3}+x+\dfrac{1}{2}+x+\dfrac{3}{5}=x+\dfrac{1}{7}+x+\dfrac{1}{4}+x+\dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{11}{10}=\dfrac{11}{28}\) (vô lý)
Vậy pt vô nghiệm
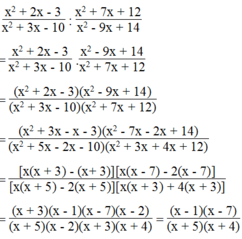
`@` `\text {Ans}`
`\downarrow`
\(9x^{10}-7x^9=0\)
`\Leftrightarrow x^9(9x-7)=0`
`\Leftrightarrow `\(\left[{}\begin{matrix}x^9=0\\9x-7=0\end{matrix}\right.\)
`\Leftrightarrow `\(\left[{}\begin{matrix}x=0\\9x=7\end{matrix}\right.\)
`\Leftrightarrow `\(\left[{}\begin{matrix}x=0\\x=\dfrac{7}{9}\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `x \in {0; 7/9}.`
F(\(x\)) = 9\(x^{10}\) - 7\(x^9\)
Nghiệm của F(\(x\)) là giá trị của \(x\) thỏa mãn F(\(x\)) = 0
⇔ 9\(x^{10}\) - 7\(x^9\) = 0
⇒ \(x^9\)\(\times\)(9\(x\) - 7) = 0
⇒ \(\left[{}\begin{matrix}x^9=0\\9x-7=0\end{matrix}\right.\)
⇒\(\left[{}\begin{matrix}x=0\\9x=7\end{matrix}\right.\)
⇒ \(\left[{}\begin{matrix}x=0\\x=\dfrac{7}{9}\end{matrix}\right.\)
Vậy nghiệm của 9\(x^{10}\) - 7\(x^9\) là : \(x\) \(\in\){0 ; \(\dfrac{7}{9}\)}