Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho biết:\(t_2=5h30';t_1=5h;s_{AB}=15km;v_1=20\left(\dfrac{km}{h}\right)\)
Điều cần tính:\(v=?\left(\dfrac{km}{h}\right);v_2=?\)
a,Thời gian ca nô chuyển động từ A đến B là:
\(\Delta t=t_2-t_1=5h30'-5h=30'=0,5h\)
Vận tốc của ca nô đó là;
\(v=\dfrac{s_{AB}}{\Delta t}=\dfrac{15}{0,5}=30\)(km/h)
b,Vận tốc trung bình của cano là:
\(v=\dfrac{s_{AB}}{t}=\dfrac{\dfrac{t}{2}\left(v_1+v_2\right)}{t}=\dfrac{1}{2}\left(20+v_2\right)=30\left(\dfrac{km}{h}\right)\)
\(\Rightarrow\dfrac{1}{2}\left(20+v_2\right)=30\Rightarrow v_2=40\left(\dfrac{km}{h}\right)\)
Vậy ...
a,Đổi 5h30 = 5,5h
Thời gian cano đi từ A đến B là:
5,5-5 = 0,5 (h)
Vận tốc của ca nô là:
\(v=\dfrac{s}{t}=\dfrac{15}{0,5}=30\left(km/h\right)\)
b) Quãng đường mà ca nô đi được trong nửa thời gian đầu là:
s1 = v1.t1 = 0,5:2.20 = 5 (km)
Vận tốc của ca nô ở nửa thời gian sau là:
\(v_2=\dfrac{s_2}{t_2}=\dfrac{s-s_1}{t-t_1}=\dfrac{15-5}{0,5-0,25}=40\left(km/h\right)\)

Đáp án D
- Thời gian xuôi dòng của canô là :
8 giờ 15 phút – 7 giờ 30 phút = 45 (phút) = 0,75 (giờ)
- Khoảng cách từ bến A đến bến B là:
25.0,75 = 18,75 (km)
- Vận tốc ca nô khi ngược dòng từ B về A là:
25 – 2.2,5 = 20 (km/h)
- Thời gian ngược dòng của canô là :
18,75 : 20 = 0,9375 (giờ) = 56 phút 15 giây
- Canô đến bến B lúc :
8 giờ 15 phút + 15 phút + 56 phút 15 giây = 9 giờ 26 phút 15 giây

a)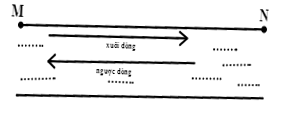
Gọi: Vận tốc của ca nô khi nước đứng yên là x.
Vận tốc của dòng nước chảy là y.
(x,y>0;km/h)(x,y>0;km/h)
Thời gian ca nô chạy ngược dòng từ N về M:
4+2=6 (giờ)
Khi ca nô chạy xuôi dòng từ M đến N ta có phương trình:
x+y=120/4=30 (1)
Khi ca nô chạy ngược dòng từ N về M ta có phương trình:
x−y=120/6=20 (2)
Từ (1) và (2) ta có hệ phương trình:
x+y=30 ; x−y=20
⇔{2x=50 ; 2y=10
⇔{x=25(n) ; y=5(n)
Vậy: Vận tốc của ca nô khi nước đứng yên là 25 km/h.
Vận tốc của dòng nước là 5 km/h.
b)
Khi ca nô tắt máy đi từ M đến N thì khi đó ca nô di chuyển là do dòng nước chảy. Vậy thời gian ca nô tắt máy đi từ M đến N là:
120:5=24 (giờ)

gọi t là thời gian đi của ca nô cũng như của thuyền ( đến B cùng lúc )
gọi vận tốc của nước đối với bờ là x
vậy vận tốc của thuyền là 3-x (km/h
............................ ca nô .... : 10+x(km/h)
vì quãng đường ca nô đi được gấp 4 lần quả đường thuyền đi nên ta có phương trình :
4*t*(3-x)=(10+x) *t
<=> 4*(3-x)= 10+x
=. x=0.4 km/h
nếu nước chảy nhanh hơn thì thời gian đi thay đổi vì x tăng => v của ca nô hay thuyền thay đổi => thời gian thay đổi !

Gọi vận tốc dòng nước là v2, vận tốc canô là v1
\(t_1=\frac{AB}{v_1+v_2};t_2=\frac{AB}{v_1-v_2}\)
\(v_{tb}=\frac{AB+AB}{\frac{AB}{v_1+v_2}+\frac{AB}{v_1-v_2}}=\frac{2AB}{AB\left(\frac{1}{v_1+v_2}+\frac{1}{v_1-v_2}\right)}=\frac{2}{\frac{\left(v_1-v_2\right)+\left(v_1+v_2\right)}{\left(v_1-v_2\right)\left(v_1+v_2\right)}}\)
\(=\frac{2\left(v_1-v_2\right)\left(v_1+v_2\right)}{2.v_1}=\frac{v_1^2-v_2^2}{v_1}=v_1-\frac{v_2^2}{v_1}\)
Do đó \(v_2\) càng nhỏ thì \(v_{tb}\)càng lớn
Vậy nước chảy chậm thì ...

a,\(\Rightarrow SMN=\left(v1+v2\right)t=4\left(v1+v2\right)\left(1\right)\)
\(\Rightarrow SMN=\left(v1-v2\right)\left(t+2\right)=6\left(v1-v2\right)\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\left\{{}\begin{matrix}v1+v2=\dfrac{120}{4}=30\\v1-v2=\dfrac{120}{6}=20\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}v1=25km/h\\v2=5km/h\end{matrix}\right.\)
b,\(\Rightarrow t=\dfrac{120}{v2}=\dfrac{120}{5}=24h\)

- Để vận tốc trung bình không thay đổi thì nước sông phản chậm hay là lặng để vận tốc đi và về là như nhau .

Giữa hai bến sông A và B cách nhau 20km theo đường thẳng có một đoàn cano phục vụ chở khách liên tục, chuyển động đều với vận tốc như sau: 20km/h khi xuôi ...

gọi vận tốc ca nô và nước lần lượt là vc và vn
khi đi ngc vc-vn
xuôi vc+vn
ta có \(2=\dfrac{AB}{v_c+v_n}\left(1\right)\)
\(3=\dfrac{AB}{v_c-v_n}\)
chia 2 vế của hai pt trên đc
\(\dfrac{2}{3}=\dfrac{v_c-v_n}{v_c+v_n}\Rightarrow v_c=5v_n\left(2\right)\)
thời gian gỗ trôi \(t=\dfrac{AB}{v_n}\Rightarrow AB=t.v_n\left(3\right)\)
(1) và (3) \(\dfrac{t.v_n}{v_n+v_c}=2\) kết hợp 2
\(\Rightarrow\dfrac{t}{6}=2\Rightarrow t=12\left(h\right)\)
lâu vc =))

Gọi thời gian khi ca nô B xuất phát từ bến là t (giờ), khi đó thời gian ca nô A đã đi được là t+1,5.
Khi gặp nhau, khoảng cách hai ca nô đã đi được bằng nhau, ta có:
v × (t+1,5) = v × 3 - v × t
=> v × (t+1,5+t) = 3v
=> v × (2t+1,5) = 3v
=> t = (3-1,5) : 2 = 0,75
Vậy, để hai ca nô đi mất thời gian bằng nhau, ca nô ở B phải xuất phát muộn hơn ca nô ở A 0,75 giờ (tức 45 phút).