NV
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 4 2017
\(\dfrac{-49}{78}\)<\(\dfrac{0}{78}\)=0=\(\dfrac{0}{-95}\)<\(\dfrac{64}{-95}\)
hông chắc nha :)
b/ sao mà so sánh cùng một lúc bốn phân số được bạn :(
23 tháng 6 2022
a: 51/56=1-5/56
61/66=1-5/66
mà -5/56<-5/66
nên 51/56<61/66
b: 41/43<1<172/165
c: \(\dfrac{101}{506}>0>-\dfrac{707}{3534}\)
18 tháng 5 2022
a: 17/200>17/314
b: 11/54=22/108<22/37
c: 141/893=3/19
159/901=3/17
mà 3/19<3/17
nên 141/893<159/901
10 tháng 12 2022
a: \(=\dfrac{-12}{7}\left(\dfrac{4}{35}+\dfrac{31}{35}\right)-\dfrac{2}{7}=\dfrac{-12}{7}-\dfrac{2}{7}=-2\)
b: =(-4)+(-4)+...+(-4)
=-4*25=-100
c: \(=157\cdot\left(-37\right)-41\cdot53+37\cdot157+51\cdot53\)
=10*53
=530
28 tháng 6 2017
a)\(\dfrac{17}{15}>1;\dfrac{29}{37}< 1\Leftrightarrow\dfrac{17}{15}>\dfrac{29}{37}\)
b) \(\dfrac{13}{17}>\dfrac{13}{18}\Leftrightarrow\dfrac{13}{17}>\dfrac{12}{18}\)
d)\(1-\dfrac{2017}{2018}=\dfrac{1}{2018}\)
\(1-\dfrac{2018}{2019}=\dfrac{1}{2019}\)
\(\dfrac{1}{2018}>\dfrac{1}{2019}\Leftrightarrow\dfrac{2017}{2018}< \dfrac{2018}{2019}\)
e) \(\dfrac{2018}{2017}< 1;\dfrac{2019}{2018}>1\Leftrightarrow\dfrac{2018}{2017}< \dfrac{2019}{2018}\)
7 tháng 4 2017
a) (1/7.x-2/7).(-1/5.x-2/5)=0
=> 1/7.x-2/7=0hoặc-1/5.x-2/5=0
*1/7.x-2/7=0
1/7.x=0+2/7
1/7.x=2/7
x=2/7:1/7
x=2
b)1/6.x+1/10.x-4/5.x+1=0
(1/6+1/10-4/5).x+1=0
(1/6+1/10-4/5).x=0-1
(1/6+1/10-4/5).x=-1
(-8/15).x=-1
x=-1:(-8/15) =15/8
24 tháng 3 2017
Ta có: \(P=\dfrac{1}{49}+\dfrac{2}{48}+\dfrac{3}{47}+...+\dfrac{48}{2}+\dfrac{49}{1}\)
\(P=\left(1+\dfrac{1}{49}\right)+\left(1+\dfrac{2}{48}\right)+\left(1+\dfrac{3}{47}\right)+...+\left(1+\dfrac{48}{2}\right)+1\)
\(P=\dfrac{50}{49}+\dfrac{50}{48}+\dfrac{50}{47}+...+\dfrac{50}{2}+\dfrac{50}{50}\)
\(P=50\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{50}\right)\)
\(\Rightarrow\dfrac{S}{P}=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{50}}{50\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{50}\right)}=\dfrac{1}{50}\)
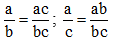
Ta có:
\(\dfrac{37}{51}< \dfrac{43}{51}\)
\(\dfrac{43}{51}< \dfrac{43}{49}\)
Do đó \(\dfrac{37}{51}< \dfrac{43}{49}\)
.