
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(x^2-8x+16=0\Leftrightarrow\left(x-4\right)^2=0\Leftrightarrow x=4\)
\(\left\{{}\begin{matrix}x-2y=-1\\3x-4y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2y-1\\3\left(2y-1\right)-4y=9\end{matrix}\right.\left\{{}\begin{matrix}x=11\\y=6\end{matrix}\right.\)

a, thay m = 3 vào pt , ta đc
x2 - 2x + 3 = 0
\(\Leftrightarrow\left(x-1\right)^2+2=0\)
Mà (x-1)2 + 2 > 0 \(\forall x\)
=> pt vô nghiệm
b, \(\Delta^'=1-m\)
pt vô nghiệm khi \(\Delta^'< 0=>m>1\)
c, pt có 2 nghiệm pb \(\Leftrightarrow\)\(\Delta^'>0\)=> 1 - m>0 => m < 1
#mã mã#

Bài 1:
a) Thay m=3 vào (1), ta được:
\(x^2-4x+3=0\)
a=1; b=-4; c=3
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{3}{1}=3\)
Bài 2:
a) Thay m=0 vào (2), ta được:
\(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
hay x=1

`x^2 -x=12`
`<=>x^2 -x-12=0`
`<=> x^2+3x-4x-12=0`
`<=> x(x+3)-4(x+3)=0`
`<=>(x+3)(x-4)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=4\end{matrix}\right.\)
`---`
`2x^2-3x=15-4x`
`<=> 2x^2-3x+4x=15`
`<=>2x^2 +x-15=0`
`<=>2x^2+6x-5x-15=0`
`<=> 2x(x+3)-5(x+3)=0`
`<=>(x+3)(2x-5)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\2x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{5}{2}\end{matrix}\right.\)
`---`
`x(x-5)=24`
`<=> x^2 -5x-24=0`
`<=>x^2+3x-8x-24=0`
`<=>x(x+3) -8(x+3)=0`
`<=>(x+3)(x-8)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=8\end{matrix}\right.\)
`----`
`x(x-3)=10(x-4)`
`<=> x^2 -3x =10x -40`
`<=>x^2 -3x-10x +40=0`
`<=> x^2 -13x+40=0`
`<=>x^2-5x-8x+40=0`
`<=> x (x-5) - 8(x-5)=0`
`<=>(x-5)(x-8)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=8\end{matrix}\right.\)
5. \(x^2-x=12\Leftrightarrow x^2-x-12=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
6. \(2x^2-3x=15-4x\Leftrightarrow2x^2+x-15=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-3\end{matrix}\right.\)
7. \(x\left(x-5\right)=24\Leftrightarrow x^2-5x-24=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-3\end{matrix}\right.\)
8. \(x\left(x-3\right)=10\left(x-4\right)\Leftrightarrow x^2-3x=10x-40\)
\(\Leftrightarrow x^2-13x+40=0\Leftrightarrow\left[{}\begin{matrix}x=8\\x=5\end{matrix}\right.\)

\(x^2+2x+m^3-3m+3=0\)
\(\Delta'=1-\left(m^3-3m+3\right)\ge0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m\le-2\end{matrix}\right.\)
Theo hệ thức Vi-et ta có \(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=m^3-3m+3\end{matrix}\right.\)
Ta có \(x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\)
\(\Leftrightarrow-8+6\left(m^3-3m+3\right)=10\)
\(\Leftrightarrow6m^3-18m=0\Leftrightarrow m=-\sqrt{3}\)(theo đk)
Vậy...........
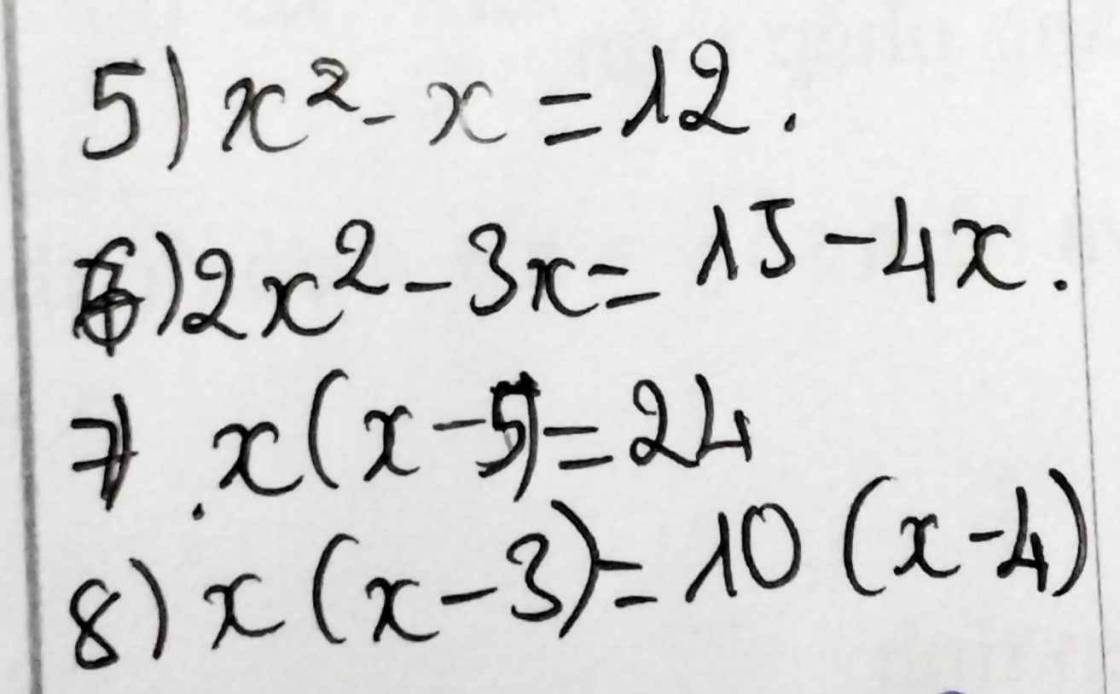
3.(2X+3)=-X.(X-2)-1 <=>6X+9=-\(x^2\)+2X-1 <=> \(x^2\) +4x+10=0 (\(\Delta\)' =4-10=-6 nhỏ hơn 0)
pt vô nghiệm