K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

7 tháng 10 2021
b: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
Suy ra: AH=DE

3 tháng 12 2021
\(a,AC=\sqrt{BC^2-AB^2}=3\sqrt{3}\left(cm\right)\\ \sin B=\dfrac{AC}{BC}=\dfrac{\sqrt{3}}{2}=\sin60^0\\ \Rightarrow\widehat{B}=60^0\\ \Rightarrow\widehat{C}=30^0\)

CM
19 tháng 9 2018
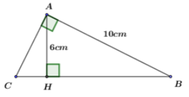
Áp dụng định lý Pytago trong tam giác ABH vuông tại H. Ta có:
![]()
Trong tam giác vuông ABC vuông tại A có AH là đường cao
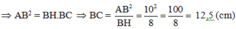
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
![]()
Vậy AC = 7,5 (cm); BC = 12,5 (cm)
Đáp án cần chọn là: B

11 tháng 1 2022
Câu 1:
a: AH=3x4:5=2,4(cm)
b: HC=16:5=3,2(cm)
Xét ΔAHC vuông tại H có
\(\sin HAC=\dfrac{HC}{AC}=\dfrac{3.2}{4}=\dfrac{4}{5}\)
nên \(\widehat{HAC}=53^0\)
A B C H
Tam giác ABH vuông tại H nên \(BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-3^2}=3\sqrt{3}\left(cm\right)\)
Tam giác ABC vuông tại A có đường cao AH nên \(AB^2=BH.BC\Rightarrow BC=\dfrac{AH^2}{BH}=\dfrac{6^2}{3\sqrt{3}}=4\sqrt{3}\left(cm\right)\)
Vậy \(BC=4\sqrt{3}\left(cm\right)\)
Tam giác ABH vuông tại H
=> BH = \(\sqrt{AB^2-AH^2}=\sqrt{6^2-3^2}=3\sqrt{3}\left(cm\right)\)
Tam giác ABC vuông tại H, đường cao AH
=> AB2 = BH.BC
Hay 62 = \(3\sqrt{3}\) . BC
=> BC = \(\dfrac{6^2}{3\sqrt{3}}\) = \(4\sqrt{3}\) (cm)
Vậy BC = \(4\sqrt{3}\) (cm)