Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

GTLN, GTNN với bảng biến thiên, đồ thị SVIP
Cho hàm số f(x) xác định, liên tục trên R và có bảng biến thiên sau:
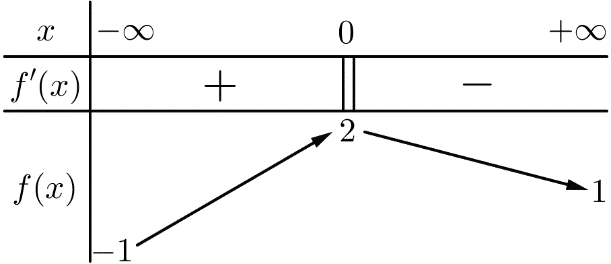
Mệnh đề nào sau đây đúng?
Cho hàm số f(x) xác định, liên tục trên R và có bảng biến thiên sau:
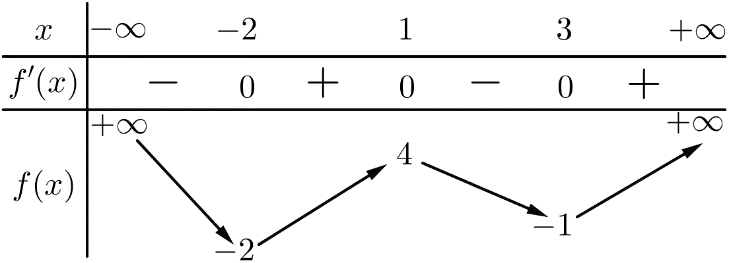
Mệnh đề nào sau đây sai?
Cho hàm số f(x) xác định, liên tục trên R và có bảng biến thiên sau:
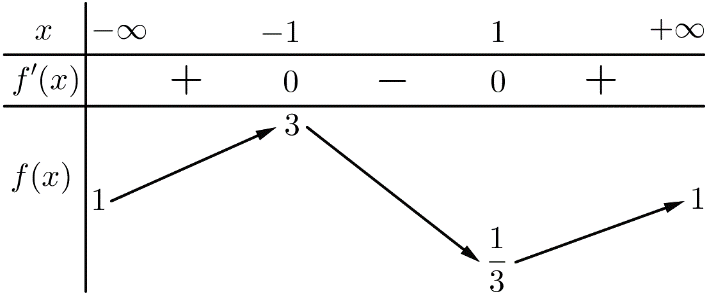
Mệnh đề nào sau đây đúng?
Cho hàm số f(x) xác định, liên tục trên R và có bảng biến thiên như sau:
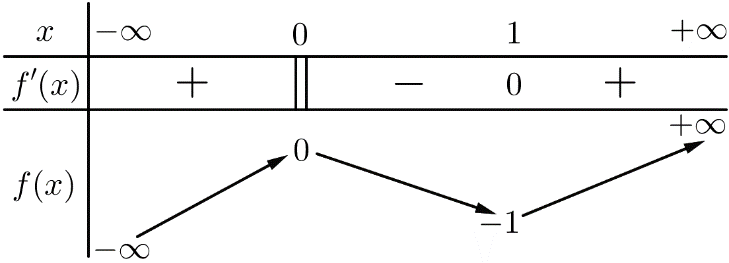
Mệnh đề nào sau đây đúng?
Cho hàm số f(x) xác định, liên tục trên R và có bảng biến thiên sau:
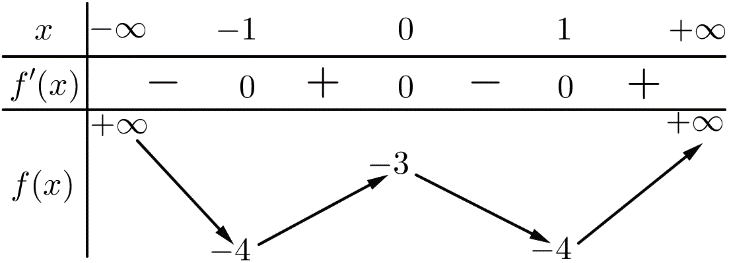
Mệnh đề nào sau đây đúng?
Cho hàm số f(x) liên tục trên R\{0} và có bảng biến thiên như sau:
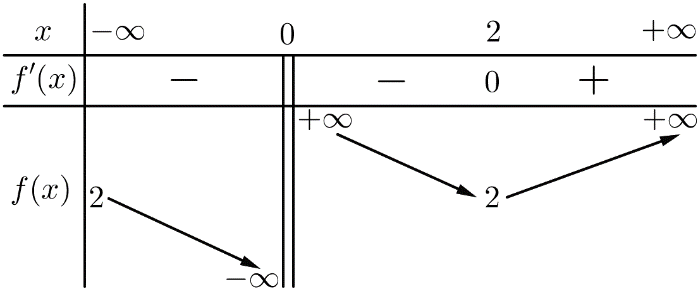
Mệnh đề nào sau đây đúng?
Cho hàm số f(x) xác định và liên tục trên [−5;7), có bảng biến thiên sau:
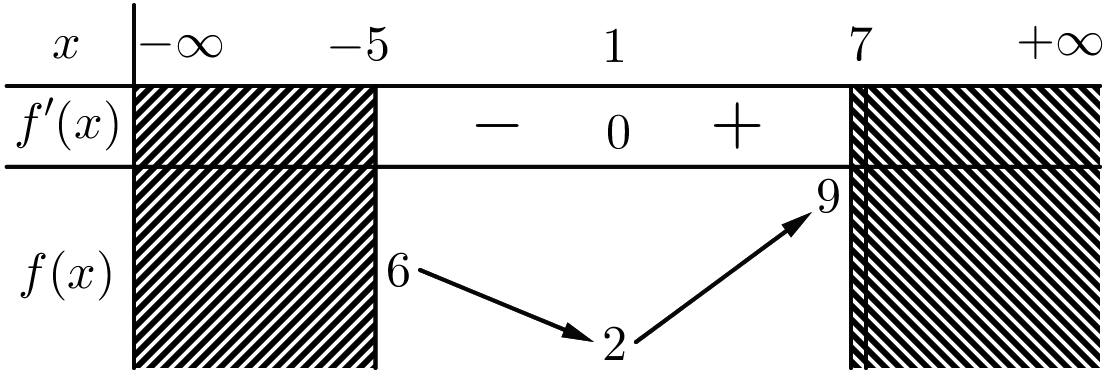
Mệnh đề nào sau đây đúng?
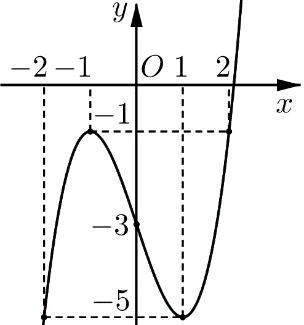
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn [−2;2] lần lượt là
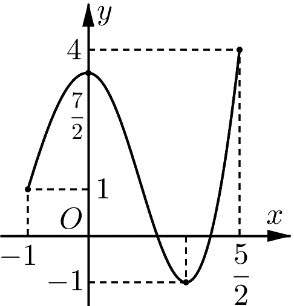
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ. Giá trị nhỏ nhất và lớn nhất của hàm số trên đoạn [−1;25] lần lượt là
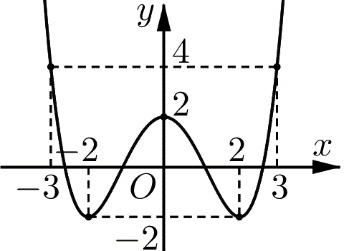
Cho hàm số f(x) có đồ thị như hình bên. Giá trị lớn nhất của hàm số f(x) trên đoạn [−2;3] bằng
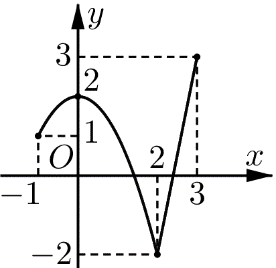
Cho hàm số f(x) liên tục trên đoạn [−1;3] và có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên [−1;3]. Giá trị của M+m bằng
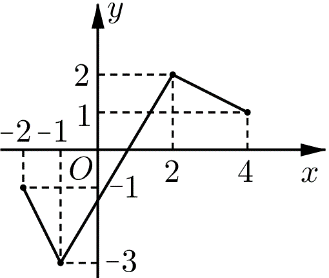
Cho hàm số y=f(x) có đồ thị trên đoạn [−2;4] như hình vẽ. Giá trị lớn nhất của hàm số y=∣f(x)∣ trên đoạn [−2;4] bằng
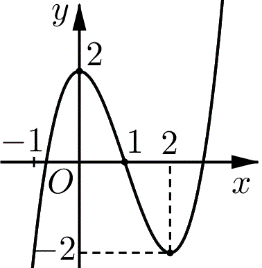
Cho hàm số bậc ba f(x) có đồ thị như hình bên. Trong các mệnh đề sau, có bao nhiêu mệnh đề sai?
i) Hàm số có hai điểm cực trị.
ii) Hàm số có GTLN là 2 và GTNN là −2.
iii) Hàm số đồng biến trên (−∞;0) và (2;+∞).
iv) Đồ thị hàm số có hai điểm cực trị: (0;2) và (2;−2).
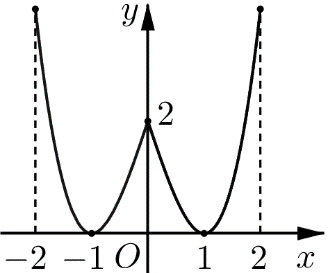
Cho hàm số f(x) liên tục trên đoạn [−2;2] và có đồ thị như hình vẽ bên. Trong các mệnh đề sau, có bao nhiêu mệnh đề đúng?
i) Hàm số nghịch biến trên khoảng (0;1).
ii) Hàm số đồng biến trên khoảng (−1;2).
iii) Trên đoạn [−2;2] hàm số có ba điểm cực trị.
iv) Trên đoạn [−2;2] hàm số có giá trị lớn nhất bằng 2.
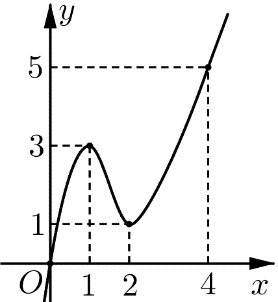
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ trên. Gọi M,m lần lượt là GTLN – GTNN của hàm số g(x)=f[2(sin4x+cos4x)]. Tổng M+m bằng

Bạn có thể đăng câu hỏi về bài học này ở đây
