Câu hỏi của Võ Thị Kim Dung

Question

Tính diện tích hình phẳng giới hạn bởi các đường:

a) y = X², y = x + 2; b) y = |lnx|, y = 1; c) y = (x – 6)², y = 6x– x²

Võ Đông Anh Tuấn · Accepted Answer

a) Phương trình hoành độ giao điểm f(x) = X²- x - 2 =0 ⇔ x = -1 hoặc x = 2.

Diện tích hình phẳng cần tìm là :

$S=\int_{-1}^{2}\left |x^{2}- x- 2 \right |dx = \left | \int_{-1}^{2}\left (x^{2}- x- 2 \right ) dx \right |$

$=\left |\frac{x^{3}}{3}-\frac{x^{2}}{2}-2x|_{-1}^{2} \right |=\left |\frac{8}{3}-2-4-(\frac{1}{3}-\frac{1}{2}+2) \right |=4\tfrac{1}{2}$

b) Phương trình hoành độ giao điểm:

f(x) = 1 - ln|x| = 0 ⇔ lnx = ± 1

⇔ x = e hoặc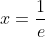 $x = \frac{1}{e}$

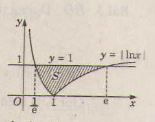
y = ln|x| = lnx nếu lnx ≥ 0 tức là x ≥ 1.

hoặc y = ln|x| = - lnx nếu x < 0, tức là 0 < x < 1.

Dựa vào đồ thị hàm số vẽ ở hình trên ta có diện tích cần tìm là :

$S=\int_{\frac{1}{e}}^{e}|1- ln|x||dx =\int_{\frac{1}{e}}^{e}(1+lnx)dx +\int_{1}^{e}(1-lnx)dx$

$= x|_{\frac{1}{e}}^{e}+\int_{\frac{1}{e}}^{e}lnxdx +x|_{1}^{e}-\int_{1}^{e}lnxdx$

$=-\frac{1}{e}+e+\int_{\frac{1}{e}}^{e}lndx-\int_{1}^{e}lnxdx$

Ta có ∫lnxdx = xlnx - ∫dx = xlnx – x + C, thay vào trên ta được :

$S=e-\frac{1}{e}+(xlnx-x)|_{\frac{1}{e}}^{e}- (xlnx-x)|_{1}^{e}=e+\frac{1}{e}-2$

c) Phương trình hoành độ giao điểm là:

f(x) = 6x – x² – (x - 6)² = -2(x² – 9x +18)

f(x) = 0 ⇔ -2(x² – 9x +18) ⇔ x = 3 hoặc x = 6.

Diện tích cần tìm là:

$S=\int_{3}^{6}|-2(x^{2}-9x+18)|dx=|2\int_{3}^{6}(x^{2}-9x+18)dx|$

$\left |=2(\frac{x^{3}}{3}-\frac{9}{2}x^{2}+18x)|_{3}^{6} \right |=9$

Câu trả lời: