Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(\dfrac{-10}{3}\right)^5.\left(\dfrac{6}{5}\right)^4\\ =\left(\dfrac{-10}{3}\right).\left(\dfrac{10}{3}\right)^4.\left(\dfrac{6}{5}\right)^4\\ =\left(\dfrac{-10}{3}\right).\left(\dfrac{10}{3}.\dfrac{6}{5}\right)^4\\ =\left(\dfrac{-10}{3}\right).4^4\\ =\left(\dfrac{-10}{3}\right).256\\ =\dfrac{-2560}{3}\)

\(\frac{16}{2^n}=2\)
=> 2n=16:2
=> 2n=8
=> 2n=23
=> n=3
b;
\(\frac{\left(-3\right)^n}{81}=-27\)
\(\Rightarrow\left(-3\right)^n=-27.81\)
=> (-3)n=-2187
=> (-3)n=(-3)7
=> n=7
c ; \(8^n:2^n=4\)
\(\Rightarrow\left(8:2\right)^n=4\)
\(\Rightarrow\left(4\right)^n=4\)
Mà : 4=41
=> 4n=41
=> n=1
![]()
\(\frac{16}{2^n}=2\)
\(16:2^n=2\)
\(2^4:2^n=2\)
\(2^n=2^4:2\)
\(2^n=2^3\)
\(=>n=3\)
\(\frac{\left(-3\right)^n}{81}=-27\)
\(\left(-3\right)^n:81=-27\)
\(\left(-3\right)^n=-27\cdot81\)
\(\left(-3\right)^n=-2187\)
\(\left(-3\right)^n=\left(-3\right)^7\)
\(=>n=7\)


Theo đề bài ta có x = , y =
( a, b, m ∈ Z, m > 0)
Vì x < y nên ta suy ra a< b
Ta có : x = , y =
; z =
Vì a < b => a + a < a +b => 2a < a + b
Do 2a< a +b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a+b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z< y
Theo đề bài ta có x = a/m, y = b/m (a, b, m ∈ Z, b # 0)
Vì x < y nên ta suy ra a < b
Ta có: x = 2a/2m, y = 2b/2m; z = (a+b)/2m
Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z < y

Theo đề bài ta có x = a/m, y = b/m (a, b, m ∈ Z, b # 0)
Vì x < y nên ta suy ra a < b
Ta có: x = 2a/2m, y = 2b/2m; z = (a+b)/2m
Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z < y

Theo đề bài ta có x = a/m, y = b/m (a, b, m ∈ Z, b # 0)
Vì x < y nên ta suy ra a < b
Ta có: x = 2a/2m, y = 2b/2m; z = (a+b)/2m
Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z < y

\(\frac{2^7.9^3}{6^5.8^2}=\frac{2^7.\left(3^2\right)^3}{\left(2.3\right)^5.\left(2^3\right)^2}=\frac{2^7.3^6}{2^5.3^5.2^6}=\frac{2^7.3^6}{2^{11}.3^5}=\frac{3}{2^4}=\frac{3}{16}\)

Bài 1:
a) 3,2.x+(−1,2).x+2,7=−4,9;3,2.x+(−1,2).x+2,7=−4,9;
(3,2−1,2)x=−4,9−2,7(3,2−1,2)x=−4,9−2,7
2.x=−7,62.x=−7,6
x=−3,8x=−3,8
b) (−5,6). x + 2,9 . x − 3,86 = −9,8 .(−5,6). x + 2,9. x−3,86 = −9,8.
(−5,6 + 2 ,9) . x = − 9.8 + 3,86 (−5,6 + 2,9) .x = −9.8 + 3,86
−2,7 .x = −5,94 − 2,7.x = −5,94
x = 2,2
Bài 2:
a) Theo định nghĩa tập số hữu tỉ là tập hợp các số có thể viết dưới dạng phân số. Hay số hữu tỉ gồm các số thập phân hữu hạn và các số thập phân vô hạn tuần hoàn.
Số vô tỉ là tập hợp gồm các số thập phân vô hạn không tuần hoàn.
Do đó: Q ∩ I = ∅
b) Số thực là tập hợp gồm số hữu tỉ và số tỉ.
Do đó: R ∩ I = I
bài 3:
a) −3,02<−3,01
b) −7,508 > −7,513
c) −0,49854 < −0,49826
d) −1,90765 < −1,892.
Bài 4:
a) −3,2 < −1,5 < −1/2 < 0 < 1 < 7,4.
b) |0| <∣−12∣ < |1 | < |−1,5| < |−3,2| < |7,4|.
Bài 7:
3 ![]() Q 3
Q 3 ![]() R 3
R 3 ![]() I
I
−2,53 ![]() Q 0,2(35)
Q 0,2(35) ![]() I N
I N ![]() Z I
Z I ![]() R
R
Bài 5:
a)Đúng b ) Sai c)Đúng
Bài 6:
a) Nếu a là số thực thì a là số hữu tỉ hoặc số vô tỉ.
b) Nếu b là số vô tỉ thì b viết được dưới dạng số thập phân vô hạn không tuần hoàn.
Bài 8:
Các số được điền vào là các số có khoanh tròn trong bảng dưới đây:
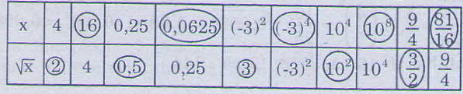
Bài 9:
a) √36=6
b) −√16=−4
c) √925=35
d) √32=3
e) √(−3)2=√9=3.
Bài 10:
D:16




thanks bn nha



