Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
trở thành một hằng đảng thức. Giá trị trong ô vuông là:
Câu 9.
a) Ta có: \(\left(a-1\right)^2\ge0\)(điều hiển nhiên)
\(\Leftrightarrow a^2-2a+1\ge0\)
\(\Leftrightarrow a^2+2a+1\ge4a\)
\(\Leftrightarrow\left(a+1\right)^2\ge4a\left(đpcm\right)\)
b) Áp dụng BĐT Cauchy cho 2 số không âm:
\(a+1\ge2\sqrt{a}\)
\(b+1\ge2\sqrt{b}\)
\(c+1\ge2\sqrt{c}\)
\(\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge8\sqrt{abc}=8\)(Vì abc = 1)
Câu 10.
a) Ta có: \(-\left(a-b\right)^2\le0\)(điều hiển nhiên)
\(\Leftrightarrow-a^2+2ab-b^2\le0\)
\(\Leftrightarrow a^2+2ab+b^2\le2a^2+2b^2\)
\(\Leftrightarrow\left(a+b\right)^2\le2\left(a^2+b^2\right)\)
b) \(\left(a+b+c\right)^2=a^2+b^2+c^2+2ab+2bc+2ac\)
Có: \(2ab\le a^2+b^2;2bc\le b^2+c^2;2ac\le a^2+c^2\)(BĐT Cauchy)
\(\Rightarrow a^2+b^2+c^2+2ab+2bc+2ac\le3\left(a^2+b^2+c^2\right)\)
Vậy \(\left(a+b+c\right)^2\le3\left(a^2+b^2+c^2\right)\)
\(a,2x^3-8x^2+8x\)
\(=2x^3-4x^2-4x^2+8x\)
\(=\left(2x^3-4x^2\right)-\left(4x^2-8x\right)\)
\(=2x\left(x-2\right)-4x\left(x-2\right)\)
\(=\left(2x-4x\right)\left(x-2\right)\)
\(b,2x^2-3x-5=2x^2-5x+2x-5\)
\(=\left(2x^2-5x\right)+\left(2x-5\right)=x\left(2x-5\right)+\left(2x-5\right)\)
\(=\left(x+1\right)\left(2x-5\right)\)
\(c,x^2y-x^3-9y+9x\)
\(=\left(x^2y-x^3\right)-\left(9y-9x\right)\)
\(=x^2\left(y-x\right)-9\left(y-x\right)\)
\(=\left(x^2-9\right)\left(y-x\right)\)
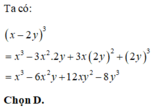
đề khó đấy
Câu 1 : sửa x^3 - 8y^3
chọn C
Câu 2 : B