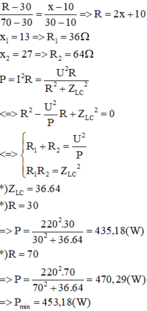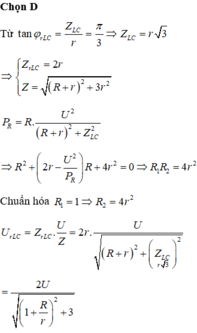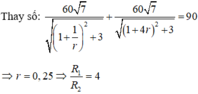Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
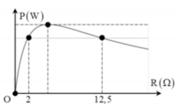
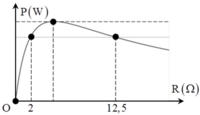
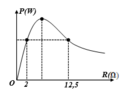
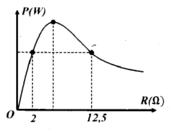
Từ đồ thị ta thấy hai giá trị của biến trở R = R 1 hoặc R = R 2 cho cùng công suất là P 0
P
=
R
I
2
=
R
.
ξ
2
R
+
r
2
=
ξ
2
R
+
r
R
⏟
≥
2
r
2
=
max
⇔
R
=
r
⇒
P
max
=
ξ
2
4
r
=
ξ
2
4
R
(1)
Mặt khác ta lại có P = R I 2 = R . ξ 2 R + r 2 ⇔ P ⏟ a . R 2 ⏟ x 2 + 2 r P − ξ ⏟ b . R ⏟ x + Pr 2 ⏟ c = 0
Áp dụng định lý Vi-et: x 1 . x 2 = c a ↔ R 1 . R 2 = r 2 ⇒ r = R 1 R 2 (2)
Từ (1) và (2) ta có P max = ξ 2 4 r = ξ 2 4 R = ξ 2 4 R 1 R 2 = 20 2 4 2.12 , 5 = 20 W

Đáp án C
Công suất tiêu thụ trên mạch
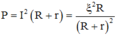
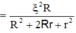
Ta thu được phương trình bậc hai với ẩn R:
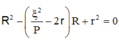
Phương trình cho ta hai nghiệm thỏa mãn ![]()
Mặt khác
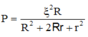
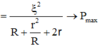
khi R = r và 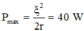

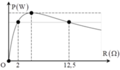
\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)