Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

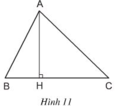
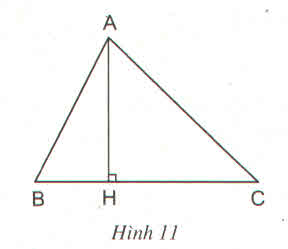
Vì AB < AC (gt) mà AB, AC là hai đường xiên có hai hình chiếu tương ứng là HB và HC nên HB > HC

.Để tập bơi nâng dần khoảng cách, hàng ngày bạn Nam xuất phát từ M, ngày thứ nhất bạn bơi đến A, ngày thứ hai bạn bơi đến B, ngày thứ ba bạn bơi đến C..(hình 12)
Hỏi rằng bạn Nam tập bơi như thế có đúng mục đích đề ra hay không ( ngày hôm sau có bơi xa hơn ngày hôm trước hay không? Vì sao?
Hướng dẫn:
Theo hình vẽ các điểm A, B, C, D nằm trên một đường thẳng d và điểm M nằm ngoài đường thẳng đó. MA là đường vuông góc kẻ từ M đến đường thẳng d. Các đoạn thẳng MB, MC, MD là các đường xiên kẻ từ M lần lượt đến B, C và D
Ta có AB, AC, AD lần lượt là hình chiếu của MB, MC, MD xuống d. Ta có ngay AD >AC > AB suy ra
MD > MC >MB > MA
Điều đó có nghĩa là ngày hôm sau bạn Nam bơi đươci xa hơn ngày hôm trước, tức là bạn Nam tập đúng mục đích đề ra

A B C E D H
Qua H kẻ đường thẳng song song AB cắt AC tại D, kẻ đường thẳng song song AC cắt AB tại E.
Ta có: \(\Delta ADH=\Delta HEA\left(g.c.g\right)\) \(\Rightarrow AD=HE;AE=HD\)
Xét \(\Delta AHD\) có HA < HD + AD, do đó HA < AE + AD (1)
Vì HE//AC, mà \(AC\perp BH\Rightarrow HE\perp BH\)
Xét tam giác vuông HBE có HB < BE (2)
Vì HD//AB, mà \(AB\perp CH\Rightarrow HD\perp CH\)
Xét tam giác vuông HCD có HC < DC (3)
Từ (1), (2), (3) suy ra:
HA + HB + HC < (AE + EB) + ( AD + DC) =AB + AC
Vậy HA + HB + HC < AB + AC (4)
Tương tự: HA + HB + HC < AB + BC (5)
HA + HB + HC < AC + BC (6)
Từ (4), (5), (6) suy ra 3(HA + HB + HC) < 2(AB + AC + BC
Vậy HA + HB + HC < \(\dfrac{2}{3}\left(AB+AC+BC\right)\)

Câu hỏi của Phạm Trung Kiên - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo nhé!

Câu hỏi của Phạm Trung Kiên - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo nhé!
Dựa vào hình vẽ, ta có:
AB, AC là hai đường xiên kẻ từ A đến BC.
HB là hình chiếu của đường xiên AB trên đường thẳng BC.
HC là hình chiếu của đường xiên AC trên đường thẳng BC.
Mà AB < AC nên HB < HC (Đường xiên nào lớn hơn thì có hình chiếu lớn hơn).
Vậy c) đúng.