Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \({\left( {x - 2} \right)^4}\)
\(\begin{array}{l} = {x^4} + 4{x^3}.\left( { - 2} \right) + 6{x^2}.{\left( { - 2} \right)^2} + 4x{\left( { - 2} \right)^3} + {\left( { - 2} \right)^4}\\ = {x^4} - 8{x^3} + 24{x^2} - 32x + 16\end{array}\)
b) \({\left( {x + 2y} \right)^5}\)
\(\begin{array}{l} = {x^5} + 5.{x^4}.\left( {2y} \right) + 10.{x^3}.{\left( {2y} \right)^2} + 10.{x^2}.{\left( {2y} \right)^3} + 5.x.{\left( {2y} \right)^4} + 1.{\left( {2y} \right)^5}\\ = {x^5} + 10{x^4}y + 40{x^3}{y^3} + 80{x^2}{y^3} + 80x{y^4} + 32{y^5}\end{array}\)

Câu 32:
Gọi M là giao điểm d1;d2 thì tọa độ M là nghiệm của hệ:
\(\left\{{}\begin{matrix}3x-5y+2=0\\5x-2y+4=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{16}{19};-\frac{2}{19}\right)\)
Do d song song d3 nên d nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình d:
\(2\left(x+\frac{16}{19}\right)-1\left(y+\frac{2}{19}\right)=0\Leftrightarrow2x-y+\frac{30}{19}=0\)
Câu 33:
\(\overrightarrow{BC}=\left(1;-2\right)\)
Do AH vuông góc BC nên AH nhận \(\left(1;-2\right)\) là 1 vtpt
Phương trình AH:
\(1\left(x+1\right)-2\left(y-2\right)=0\Leftrightarrow x-2y+5=0\)
Câu 34:
Tọa độ M là: \(M\left(\frac{3}{2};4\right)\)
\(\overrightarrow{CM}=\left(-\frac{3}{2};6\right)=-\frac{3}{2}\left(1;-4\right)\)
Phương trình tham số CM: \(\left\{{}\begin{matrix}x=3+t\\y=-2-4t\end{matrix}\right.\)
Câu 30:
\(\overrightarrow{AB}=\left(-2;0\right)=-2\left(1;0\right)\) nên đường thẳng AB nhận \(\left(1;0\right)\) là 1 vtcp
Phương trình AB: \(\left\{{}\begin{matrix}x=1+t\\y=-7\end{matrix}\right.\)
Cả 4 đáp án đều ko chính xác
Câu 31:
Gọi M là trung điểm AB \(\Rightarrow M\left(-1;1\right)\)
\(\overrightarrow{AB}=\left(-6;-4\right)=-2\left(3;2\right)\Rightarrow\) đường trung trực AB nhận \(\left(3;2\right)\) là 1vtpt
Phương trình:
\(3\left(x+1\right)+2\left(y-1\right)=0\Leftrightarrow3x+2y+1=0\)

a)Vì \(x:y:z=2:3:\left(-4\right)\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{-4}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{-4}=\frac{x-y+z}{2-3+-4}=\frac{-125}{-5}=25\)
\(\Rightarrow\begin{cases}\frac{x}{2}=25\\\frac{y}{3}=25\\\frac{z}{-4}=25\end{cases}\)\(\Rightarrow\)\(\begin{cases}x=50\\y=75\\z=-100\end{cases}\)
Vậy x=50;y=75;z=-100
d)Vì 2x=3y\(\Rightarrow\frac{x}{3}=\frac{y}{2}\Rightarrow\frac{x}{21}=\frac{y}{14}\)(1)
5y=7z\(\Rightarrow\frac{y}{7}=\frac{z}{5}\Rightarrow\frac{y}{14}=\frac{z}{10}\)(2)
Từ (1) và (2) suy ra:\(\frac{x}{21}=\frac{y}{14}=\frac{z}{10}\)
Áp dụng dãy tỉ số bằng nhau ta có:
\(\Rightarrow\frac{x}{21}=\frac{y}{14}=\frac{z}{10}=\frac{3x}{63}=\frac{7y}{98}=\frac{5z}{50}=\frac{3x-7y+5z}{63-98+50}=\frac{30}{15}=2\)
\(\Rightarrow\begin{cases}\frac{x}{21}=2\\\frac{y}{14}=2\\\frac{z}{10}=2\end{cases}\)\(\Rightarrow\)\(\begin{cases}x=42\\y=28\\z=20\end{cases}\)

\(\left(x+5\right)^4+\left(x-5\right)^4=\left[\left(x+5\right)^4+2.\left(x+5\right)^2.\left(x-5\right)+\left(x-5\right)^4\right]-2.\left(x+5\right)^2\left(x-5\right)^2\)
\(=\left[\left(x+5\right)^2-\left(x-5\right)^2\right]^2-\left[\sqrt{2}\left(x+5\right)\left(x-5\right)\right]^2\)
\(=\left[\left(x+5\right)^2+\left(x-5\right)^2+\sqrt{2}\left(x+5\right)\left(x-5\right)\right]^2\)
Sau đó bạn áp dụng hằng đẳng thức thứ nhất và thứ 2 ( bình phương 1 tổng và bình phương 1 hiệu tính ra nhé


Bài 1
d, \(x^2+2xy+y^2-2x-2y+1\)
\(\Rightarrow x^2+y^2=1+2xy-2y-2x\)
\(\Rightarrow\left(x+y-1\right)^2\)
Bài 2:
a, \(\left(x+1\right)\left(x+1\right)=\left(x+2\right)\left(x+5\right)\)
\(\Leftrightarrow\left(x+1\right)^2=x^2+5x+2x+10\)
\(\Leftrightarrow x^2+2x+1=x^2=5x+2x+10\)
\(\Leftrightarrow-5x=9\)
\(\Leftrightarrow x=-\frac{9}{5}\)
b,\(\left(x+3\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-5\end{matrix}\right.\)
c, \(4x^2-9=0\)
\(\Leftrightarrow4x^2=9\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{3}{2}\\\frac{3}{2}\end{matrix}\right.\)
d,\(\left(4x-5\right)^2-\left(3x-4\right)^2=0\)
\(\Leftrightarrow16x^2-40x+25-\left(9x^2-24x+16\right)=0\)
\(\Leftrightarrow16x^2-40x+25-9x^2+24x-16=0\)
\(\Leftrightarrow7x^2-16x+9=0\)
\(\Leftrightarrow x=\frac{-\left(-16\right)\pm\sqrt{\left(-16\right)^2-4.7.9}}{14}\)
\(\Leftrightarrow x=\frac{16\pm\sqrt{256-252}}{14}\)
\(\Leftrightarrow x=\frac{16\pm\sqrt{4}}{14}\)
\(\Leftrightarrow x=\frac{16\pm2}{14}\)
\(\Leftrightarrow x=\left[{}\begin{matrix}\frac{16+2}{14}\\\frac{16-2}{14}\end{matrix}\right.\)
\(\Leftrightarrow x=\left[{}\begin{matrix}\frac{9}{7}\\1\end{matrix}\right.\)
1.a)\(3x-3y+x^2-2xy+y^2\)
\(=3\left(x-y\right)+\left(x-y\right)^2\)
\(=\left(x-y\right)\left(3+x-y\right)\)
d)\(x^2+2xy+y^2-2x-2y+1\)
\(=\left(x+y\right)^2-2\left(x+y\right)+1\)
\(=\left(x+y+1\right)^2\)
2.a)\(\left(x+1\right)\left(x+1\right)=\left(x+2\right)\left(x+5\right)\)
\(\Leftrightarrow\left(x+1\right)^2=x^2+5x+2x+10\)
\(\Leftrightarrow x^2+2x+1-x^2-7x-10=0\)
\(\Leftrightarrow-5x-9=0\)
\(\Leftrightarrow-5x=9\)
\(\Leftrightarrow x=-\frac{9}{5}\). Vậy \(S=\left\{-\frac{9}{5}\right\}\)
b)\(\left(x+3\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-5\end{matrix}\right.\).Vậy \(S=\left\{-3;-5\right\}\)
c)\(4x^2-9=0\)
\(\Leftrightarrow\left(2x+3\right)\left(2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+3=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\frac{3}{2}\\x=\frac{3}{2}\end{matrix}\right.\). Vậy \(S=\left\{\pm\frac{3}{2}\right\}\)
d)\(\left(4x-5\right)^2-\left(3x-4\right)^2=0\)
\(\Leftrightarrow\left(4x-5+3x-4\right)\left(4x-5-3x+4\right)=0\)
\(\Leftrightarrow\left(7x-9\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}7x-9=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{9}{7}\\x=1\end{matrix}\right.\). Vậy \(S=\left\{1;\frac{9}{7}\right\}\)
3.Ta có:
8x^2-26x+m 2x-3 4x-7 -14x+m m+21
Để \(A\left(x\right)⋮B\left(x\right)\) thì: \(m+21⋮2x-3\)
\(\Rightarrow m+21=0\)
\(\Rightarrow m=-21\)
Vậy...!
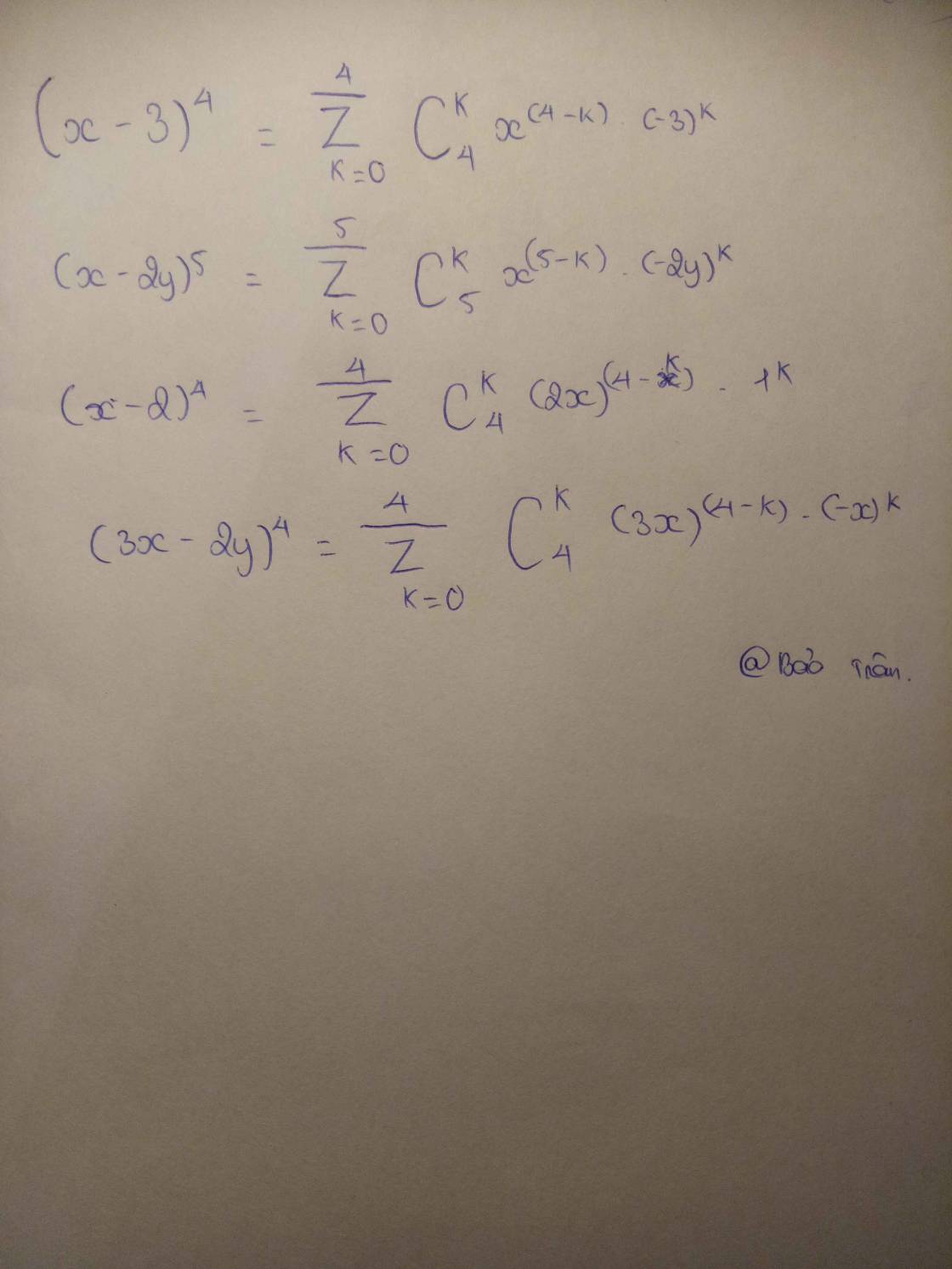

a) \(\begin{array}{l}{(x - 3)^4} = {x^4} + 4{x^3}.( - 3) + 6{x^2}.{( - 3)^2} + 4x.{( - 3)^3} + {( - 3)^4}\\ = {x^4} - 12{x^3} + 54{x^2} - 108x + 81\end{array}\)
b) \({(3x - 2y)^4} = 81{x^4} - 216{x^3}y + 216{x^2}{y^2} - 96x{y^3} + 16{y^4}\)
c)
\(\begin{array}{l}{(x + 5)^4} + {(x - 5)^4} = {x^4} + 20{x^3} + 150{x^2} + 500x + 625\\ + {x^4} - 20{x^3} + 150{x^2} - 500x + 625\\ = 2{x^4} + 300{x^2} + 1250\end{array}\)
d) \({(x - 2y)^5} = {x^5} - 10{x^4}y + 40{x^3}{y^2} - 80{x^2}{y^3} + 80x{y^4} - 32{y^5}\)