Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
+ Chu kì của con lắc vướng đinh T = π l 0 g + π 0 , 5 l 0 g = 2 , 4

Đáp án D
+ Chu kì dao động của con lắc T = π l g + π 0 , 5 l g = π 1 π 2 + π 0 , 5 π 2 = 1 + 2 2 s

Đáp án C
Phương pháp: Áp dụng công thức tính chu kì dao động của con lắc đơn
Cách giải:
Chu kì dao động của con lắc sau khi bị vướng vào đinh gồm:
+ ½ chu kì dao động với chiều dài dây l
+ ½ chu kì dao động với chiều dài dây l’ = 4l/9
Chu kì dao động của con lắc có chiều dài l: T 0 = 2 π l g
Chu kì dao động của con lắc với chiều dài dây 4l/9 là: T ' = 2 π l g
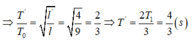
=> Chu kì dao động mới của con lắc vướng đinh là: T = (T’+ T0)/2 = 1,67s
=> Chọn C

I K O M P T N
Để vật có thể chuyển động tròn xung quanh đinh thì nó phải qua điểm M.
Tại M, lực tác dụng lên vật gồm trọng lực P, lực căng T
Áp dụng định luật 2 Niu tơn, ta có: \(m\vec{a}=\overrightarrow{P}+\overrightarrow{T}\)
Chiếu lên phương hướng tâm, ta có: \(m.a_{ht}=P+T\Rightarrow T=m.a_{ht}-mg\)
Để vật đi qua M thì T > 0 \(\Rightarrow a_{ht}>g\Leftrightarrow\frac{v^2}{L}>g\)(*)
Mặt khác, áp dụng định luật bảo toàn cơ năng ta có: \(W_N=W_M\Leftrightarrow mgl\left(1-\cos\alpha_0\right)=mg.2L+\frac{1}{2}mv^2\)
\(\Rightarrow v^2=2gl\left(1-\cos\alpha_0\right)-4gL\)
Thay vào (*) ta đc: \(\frac{2gl\left(1-\cos\alpha_0\right)}{L}-4g>g\Leftrightarrow L<\frac{2l\left(1-\cos\alpha_0\right)}{5}\)
Thay số, ta đc: \(L<\frac{2.1.\left(1-\cos75\right)}{5}=0,276m\)

Đáp án C
+ Việc vướng đinh không làm thay đổi cơ năng của con lắc, do vậy ta luôn có:
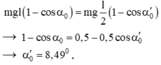
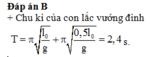


Khi không vướng đinh thì chu kì là: \(T_1=2\pi\sqrt{\dfrac{\ell}{g}}=2\pi\sqrt{\dfrac{1}{10}}=2s\)
Khi vướng đinh thì chu kì là:\(T_2=2\pi\sqrt{\dfrac{\ell_2}{g}}=2\pi\sqrt{\dfrac{0,64}{10}}=1,6s\)
Chu kì của con lắc gồm 1 nửa bị vướng đinh, một nửa không vướng đinh:
\(T=\dfrac{T_1+T_2}{2}=1,8s\)