Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

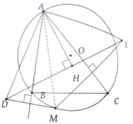
Do D đối xứng M qua AB \(\Rightarrow\) AB là trung trực DM
\(\Rightarrow AM=AD\) và \(\widehat{DAB}=\widehat{MAB}\)
Tương tự ta có \(AM=AE\) và \(\widehat{CAM}=\widehat{CAE}\)
\(\Rightarrow\widehat{DAE}=\widehat{DAB}+\widehat{MAB}+\widehat{CAM}+\widehat{CAE}=2\left(\widehat{MAB}+\widehat{CAM}\right)=2\widehat{BAC}\)
Do \(AM=AD=AE\Rightarrow\Delta ADE\) cân tại A
Kẻ đường cao AH ứng với DE \(\Rightarrow\) H đồng thời là trung điểm DE và \(\widehat{DAH}=\dfrac{1}{2}\widehat{DAE}=\dfrac{1}{2}.2\widehat{BAC}=\widehat{BAC}\)
Trong tam giác vuông ADH:
\(sin\widehat{DAH}=\dfrac{DH}{AD}\Rightarrow DH=AD.sin\widehat{DAH}=AM.sin\widehat{BAC}\)
\(\Rightarrow\dfrac{1}{2}DE=AM.sin\widehat{BAC}\Rightarrow DE=2AM.sin\widehat{BAC}\)
Mà ABC cố định \(\Rightarrow DE_{max}\) khi \(AM_{max}\Rightarrow AM\) là đường kính của đường tròn
Hay M đối xứng A qua tâm O

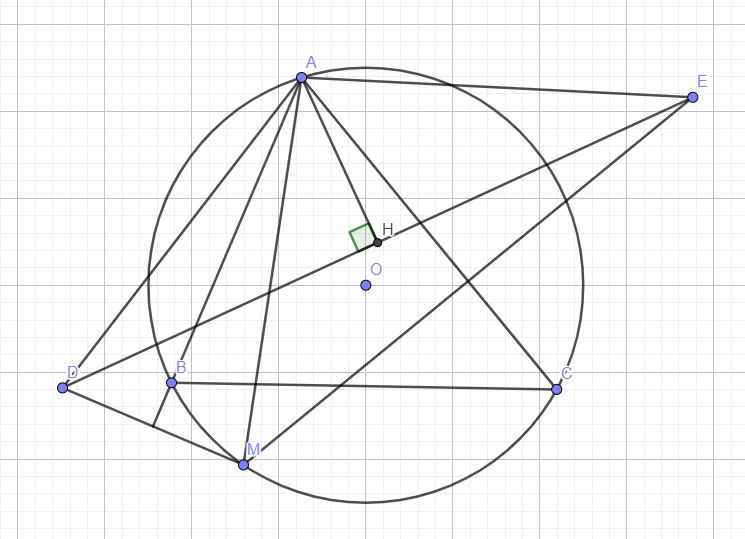
Kẻ AH ⊥ DE tại H
D A E ^ = 2 B A C ^
=> D A H ^ = B A C ^
Từ DE=2DH; AD=AM=AE
Suy ra DH=AD.sin D A H ^
Từ đó D E m a x <=> AM = 2R

1. Gọi giao điểm của CH với AB là I, AH với BC là K,Ta có tứ giác BIHK nội tiếp ⇒I^BK+K^HI=1800màK^HI=A^HC⇒I^BK+A^HC=1800 (1) Ta lại có I^BK=A^MC (hai góc nội tiếp cùng chắn một cung)
A^MC=A^PC (t/c đối xứng) ⇒I^BK=A^PC (2)Từ (1) và (2) ⇒A^PC+A^HC=1800Suy ra tứ giác AHCP nội tiếp.2. Tứ giác AHCP nội tiếp ⇒A^HP=A^CP=A^CMTa lại có A^CM+A^BM=1800⇒A^HP+A^BM=1800 mà A^BM=A^BN
⇒A^HP+A^BN=1800 (3)Chứng minh tương tự câu 1) ta có tứ giác AHBN nội tiếp
⇒A^BN=A^HN (4)
Từ (3) và (4) ⇒A^HP+A^HN=1800⇒ N, H, P thẳng hàng
3. M^AN=2B^AM;M^AP=2M^AC
=> N^AP=2(B^AM+M^AC)=2B^AC (<180độ) không đổi
Có AN = AM = AP, cần chứng minh NP = 2.AP.sinBAC
=> NP lớn nhất <=> AP lớn nhất mà AP = AM
AM lớn nhất <=> AM là đường kính của đường tròn (O)
Vậy NP lớn nhất <=> AM là đường kính của đường tròn.
a)gọi I là giao điểm của CH và AB
K là giao điểm AH và BC
ta có :góc IBK+ AHC=180 độ
mà góc IBK= APC
=> tứ giác AHCP nội tiếp
b)Ta có Góc AHP= ACP cùng chắn cung AP (
mà góc ACP=ACM (1)
=> góc ACP= AHP
cmtt
gócAHN=ABN cùng chắn cung AP
mà ABN=ABM => AHN=ABM(2)
Xét tứ giác ABMC nội tiếp
gócACM+ABM=180 độ (3)
từ (1)(2)(3) =>
góc AHP+AHN=180 độ
=> N,H,P thẳng hàng
ta có góc MAN=2BAM,
góc MAP=2MAC
=> NAP=2(BAM+MAC)
=2 x góc BAC (ko đổi )
ta có AM=AN=AP
NP=2AP.sin BAC=2AM.sinBAC
=> NP lớn nhất <=> AM Max

Tham khảo: