K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

19 tháng 7 2016
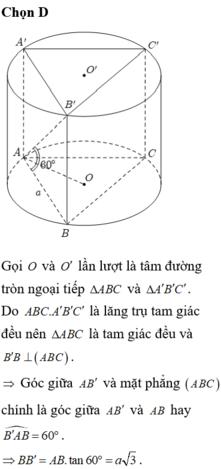
Hình bạn tự vẽ nhé
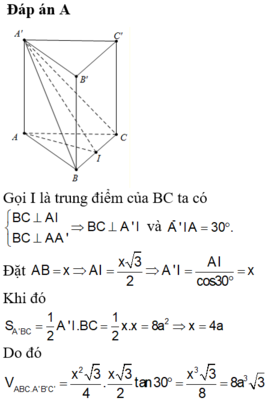
gọi M là trung điểm cạnh BC
vì là lăng trụ tam giác đều nên tam giác A'BC cân tại A' \(\Rightarrow\) A'M vuông góc với BC và AM vuông góc với BC
=> (AA'M) vuông góc ( A'BC) => góc giữa AA' và (A'BC) = góc giữa AA' và A'M = 300
xét tam giác AA'M vuông tại A có: tan30 = \(\frac{AM}{AA'}\) => AM = \(\frac{\sqrt{3}a}{3}\)
=> cạnh tam giác = \(\frac{2a}{3}\) => SABC= \(\frac{\sqrt{3}a^2}{18}\) => VABC.A'B'C'=\(AA'\times S_{ABC}\) = \(\frac{\sqrt{3}a^3}{18}\)
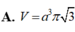
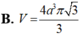
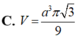
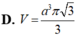

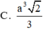
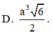

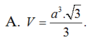
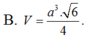
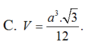
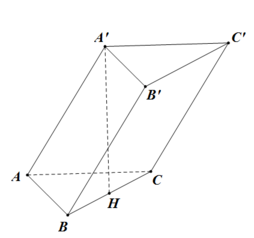
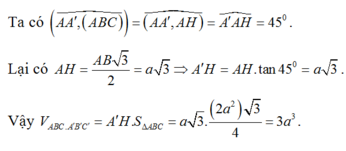

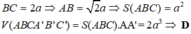


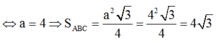
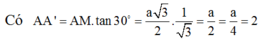

Lời giải:
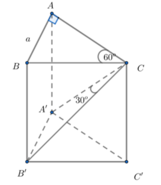
Từ $A$ kẻ $AH$ vuông góc với $BC$
Khi đó:
\(60^0=\angle ((A'BC), (ABC))=\angle (AH, A'H)=\angle AHA'\)
Do hình lăng trụ đã cho là lăng trụ đều nên tam giác $ABC$ là tam giác đều có đường cao $AH$ nên:
\(AH=\sqrt{a^2-(\frac{a}{2})^2}=\frac{\sqrt{3}a}{2}\)
\(\Rightarrow \sqrt{3}=\tan AHA'=\frac{AA'}{AH}\Rightarrow AA'=\frac{3}{2}a\)
\(V_{ABC.A'B'C'}=S_{ABC}.AA'=\frac{AH.BC}{2}.\frac{3}{2}a=\frac{\sqrt{3}a^2}{4}.\frac{3}{2}a=\frac{3\sqrt{3}a^3}{8}\)