Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ đồ thị hàm số y = x2.
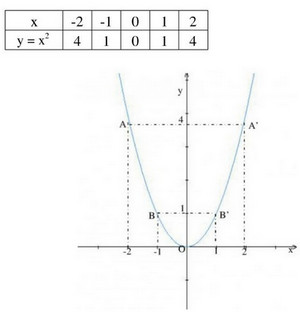
b) Ta có y = f(x) = x2 nên
f(-8) = (-8)2 = 64; f(-1,3) = (-1,3)2 = 1,69; f(-0,75) = (-0,75)2 = 0,5625; f(1,5) = 1,52 = 2,25.
c) Theo đồ thị ta có:
(0,5)2 ≈ 0,25
(-1,5)2 ≈ 2,25
(2,5)2 ≈ 6,25
d) Theo đồ thị ta có: Điểm trên trục hoành √3 thì có tung độ là y = (√3)2 = 3. Suy ra điểm biểu diễn √3 trên trục hoành bằng 1,7. Tương tự điểm biểu diễn √7 gồm bằng 2,7.

a) Vẽ đồ thị
b) Gọi yA, yB, yC lần lượt là tung độ các điểm A, B, C có cùng hoành độ x = -1,5. Ta có:
yA = . (-1,5)2 =
. 2,25 = 1,125
yB = (-1,5)2 = 2,25
yC = 2 (-1,5)2 = 2 . 2,25 = 4,5
c) Gọi yA, yB, yC’ lần lượt là tung độ các điểm A', B', C' có cùng hoành độ x = 1,5. Ta có:
yA, = . 1,52 =
. 2,25 = 1,125
yB, = 1,52 = 2,25
yC’ = 2 . 1,52 = 2 . 2,25 = 4,5
Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.
d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 nên O là điểm thấp nhất của đồ thị. Khi đó ta có x = 0.
Vậy x = 0 thì hàm số có giả trị nhỏ nhất.

chị thay vao ham so ta co;
b= -0,3.(-4)2 = -4,8
diem B(4;b) cung nam tren do thi do vi (-4)2=42=16
Biết A = (-4;b) vậy x = -4, y =b.
Thay x= -4, y = b vào hso ta đc:
b=-0.3*(-4)2=.......

a. Vẽ được rồi nên thôi
Hai điểm A(-2, 2) và B(1, 1/2)
b. Đường thẳng AB có PT: x + 2y - 2 = 0.
c. Diện tích tam giác ABC = \(\frac{1}{2}\)AB x d(C/AB)
AB cố định. => Diện tích tam giác ABC lớn nhất khi d(C/AB) lớn nhất
Điểm C có tọa độ (x; \(\frac{x^2}{2}\))
d(C/AB) = \(\frac{\left|x+2\frac{x^2}{2}-2\right|}{\sqrt{1^2+2^2}}\)
d(C/AB) đạt max khi \(\left|x+x^2-2\right|\) đạt max (vì C thuộc cung AB nên -2 < x < 1)
Ta có x2 + x - 2 = (x + 2)(x - 1)
với -2 < x < 1 => x2 + x - 2 < 0
=> \(\left|x^2+x-2\right|\)= -x2 - x + 2 (khi 2- < x < 1)
Vậy, d(C/AB) đạt max khi -x2 - x + 2 đạt max (khi 2- < x < 1)
-x2 -x + 2 = -(x + \(\frac{1}{2}\))2 + \(\frac{1}{4}\) + 2
= -(x +\(\frac{1}{2}\))2 + 9/4 >= 9/4
Vậy, d(C/AB) đạt max khi x = -\(\frac{1}{2}\)
Thay x = \(-\frac{1}{2}\)vào (P): y = \(\frac{x^2}{2}\)
Vậy, Điểm C: (\(-\frac{1}{2}\); \(\frac{1}{8}\))
b: Thay x=2 vào hàm số, ta được:
\(y=\dfrac{-1}{2}\cdot2^2=-2\)