Vì Nam muốn chia 12 viên bi xanh,18 viên bi đỏ và 30  viên bi vàng vào các túi nhiều nhất sao cho mỗi túi có đủ các loại bi nên số túi phải là ƯCLN( 12,18,30)

Ta có :

12=2².3

18=2.3²

30=2.3.5

ƯCLN(12,18,30) =2.3=6

Vậy có thể chia nhiều nhất thành 6 túi 

2

Đây là toán nâng cao chuyên đề bội ước, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:

                                    Giải:

Vì a : 9 dư 3 nên a - 3 ⋮ 9 ⇒ a - 3 + 99 ⋮ 9 ⇒ a + 96 ⋮ 9 (1)

Vì a : 27 dư 12 nên a - 12 ⋮ 27 ⇒ a - 12 + 108 ⋮ 27 ⇒ a + 96 ⋮ 27 (2)

Vì a : 41 dư 27 nên a - 27 + 123 ⋮ 41 ⇒ a + 96 ⋮ 9 (3)

Kết hợp (1); (2) và (3) ta có: a + 96 \(\in\) BC(9; 27; 41)

  9 = 3²; 27 = 3³; 41 = 41 BCNN(9; 27; 41) = 1107

⇒ a + 96 \(\in\) B(1107) = {0; 1107; ...} ⇒ a \(\in\) B(1107) = {-96; 1011;..}

Vì a là số tự nhiên và a nhỏ nhất nên a = 1011

Kết luận a = 1011

= -418-\(\left\{-218-\left[-118-200+2023\right]\right\}\)

= -418-\(\left\{-218-\left[-318+2023\right]\right\}\)

= -418-\(\left\{-218-1705\right\}\)

= -418--1923

=1505

- 418 - {218 - [-118 - (318) + 2023]}

= -418 - {218 - [-118 - 318 + 2023]}

= -418 - {218 - [- 436 + 2023]}

= - 418 - {218 - 1587}

= - 418 - (-1369)

= -418 + 1369

=  951 

\(n-2000=a^2\left(a\in N\right)\Rightarrow n=a^2+2000\left(1\right)\)

\(n-2011=b^2\left(b\in N\right)\Rightarrow n=b^2+2011\left(2\right)\)

\(\left(1\right);\left(2\right)\Rightarrow a^2+2000=b^2+2011\)

\(\Rightarrow a^2-b^2=11\)

\(\Rightarrow\left(a-b\right)\left(a+b\right)=11\)

\(\Rightarrow\left(a-b\right);\left(a+b\right)\in U\left(11\right)=\left\{1;11\right\}\)

\(\Rightarrow\left(a;b\right)=\left\{6;5\right\}\)

\(\left(1\right)\Rightarrow n=36+2000=2036\)

Kiểm tra \(\left(2\right)\Rightarrow n=25+2011=2036\left(đúng\right)\)

Vậy \(n=2036\)

    Đây là toán nâng cao chuyên đề giải phương trình nghiệm nguyên, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:

                             Giải:

Vì n - 2000 là số chính phương nên n - 2000 = k² (k \(\in\) N)

Vì n - 2011 là số chính phương nên n - 2011 = d²(d\(\in\) N); d < k

Hiệu của hai số trên là: n - 2000 - (n - 2011) = k² - d²

            n - 2000 - n + 2011 = k² - d²

           (n - n) + (2011 - 2000) = k² - d²

                0 + 11 = k²  - kd + kd - d²

                       11 = (k² - kd) + (kd - d²)

                        11 = k(k - d) + d(k -  d)

                       11 = (k - d).(k + d); Ư(11) = {1; 11} 

  Vì k; d \(\in\)  N ta có:   k - d < k + d ⇒ k - d = 1; k + d = 11

       k - d = 1 ⇒ k = 1 + d ⇒ 1  + d  + d = 11  ⇒ d + d = 11 - 1

⇒ 2d = 10 ⇒ d = 10 : 2  = 5 ⇒ n - 2011 = d² = 5² = 25

⇒ n = 2011 + 25 = 2036

Vậy n = 2036 

XẾP THÀNH 3 ,4,9 HÀNG NGHĨA LÀ SỐ HỌC SINH LỚP ĐÓ LÀ SỐ CHIA HẾT CHO 3,4,9

SUY RA : SỐ HỌC SINH LỚP ĐÓ LÀ 36

                      Giải:

Vì số học sinh lớp 6A xếp hàng 3, hàng 4 hàng 9 đều vừa đủ nên số học sinh lớp đó là bội chung của 3; 4; 9

          3 = 3; 4 = 2²; 9 = 3²

BCNN(3; 4; 9) = 2².3² = 36

Vậy số học sinh của lớp đó thuộc bội của 36

          B(36) = {0; 36; 72; ...}

Vì số học sinh của lớp đó từ 30 đến 40 nên số học sinh lớp đó là:

       36 học sinh

Kết luận: Số học sinh của lớp đó là 36 học sinh.

A = 2024⁰ + 2024²⁰²⁵ + 2024²⁰²⁶ + 2024²⁰²⁷ + 2024²⁰²⁸

A = 1 + (2024²⁰²⁵ + 2024²⁰²⁶) + (2024²⁰²⁷ + 2024²⁰²⁸)

A = 1 +  2024²⁰²⁵.(1 + 2024) + 2024²⁰²⁷.(1+ 2024)

A = 1 + (1 + 2024)(2024²⁰²⁵ + 2024²⁰²⁷) 

A = 1 + 2025.(2024²⁰²⁵ + 2024²⁰²⁷)

2025 ⋮ 2025; 1 : 2025 dư 1 

⇒ A : 2025 dư 1

Kết luận A chia 2025 dư 1

Ta có: a chia cho 24 được số dư là 10 và thương là k nên:

    a = 24k + 10 (k ∈ N)

Vì 24 ⋮ 2 và 10 ⋮ 2 nên (24k + 10) ⋮ 2

Vì 24 ⋮ 4 và 10 không chia hết cho 4 nên (24k + 10) không chia hết cho 4

Vì a : 24 dư 10 , thương gọi là k ( k  ∈ N)

A=24 x k +10

Vì 24 ⋮2 và 10 cũng ⋮ 2 nên a ⋮2

Tương tụ , 24 ⋮4 và 10  ko chia hết cho 4 nên a ko chia hết cho 4

                    Giải:

a; Mô tả yếu tố cơ bản của hình vuông:

* Các cạnh của hình vuông bằng nhau

* Bốn góc hình vuông bằng nhau và bằng 90⁰

* Đường chéo của hình vuông:

+ Hai đường chéo hình vuông bằng nhau

+ Hai đường chéo hình vuông vuông góc với nhau 

+ Hai đường chéo hình vuông cắt nhau tại trung điểm của mỗi đường.

b; Mô tả nền nhà hình chữ nhật có kích thước 8m, 6m

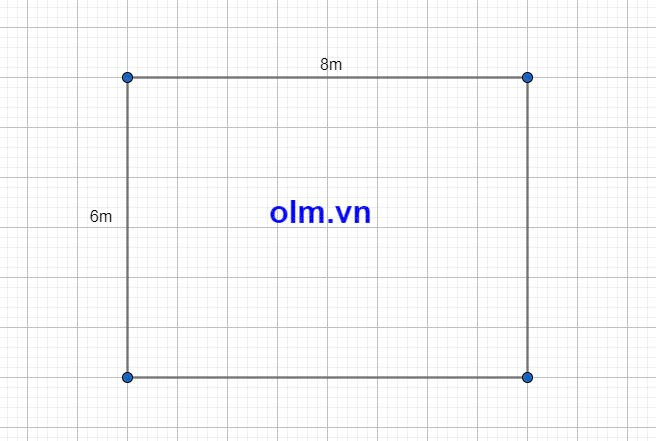
Diện tích của nền nhà là: 8 x 6 = 48 (m²)

Kết luận diện tích căn nhà là 48m²

j: \(\left(5^7+7^5\right)\left(6^8+8^6\right)\left(2^4-4^2\right)\)

\(=\left(5^7+7^5\right)\left(6^8+8^6\right)\left(16-16\right)\)

\(=0\cdot\left(5^7+7^5\right)\left(6^8+8^6\right)\)

=0

k: \(\left(7^{50}+7^{29}\right)\left(5^{14}+5^{26}\right)\left(3^{35}\cdot3-9^{18}\right)\)

\(=\left(7^{50}+7^{29}\right)\cdot\left(5^{14}+5^{26}\right)\left(3^{36}-3^{36}\right)\)

\(=\left(7^{50}+7^{29}\right)\left(5^{14}+5^{26}\right)\cdot0=0\)

a: 48-3(x+5)=24

=>3(x+5)=48-24=24

=>\(x+5=\dfrac{24}{3}=8\)

=>x=8-5=3

b: \(2^{x+1}-2^x=32\)

=>\(2\cdot2^x-2^x=32\)

=>\(2^x=32=2^5\)

=>x=5

c: \(\left(15+x\right):3=3^3\)

=>\(x+15=3^3\cdot3=3^4=81\)

=>x=81-15=66

d: \(250-10\left(24-3x\right):15=224\)

=>\(\dfrac{2}{3}\left(24-3x\right)=250-224=26\)

=>\(24-3x=26:\dfrac{2}{3}=26\cdot\dfrac{3}{2}=39\)

=>3x=24-39=-15

=>\(x=-\dfrac{15}{3}=-5\)