A. S

B. S

C. Đ

D. Đ

a.s

b.s

c.đ

d.đ

nhé tick cho mình nhé

Số học sinh nữ kém hơn số học sinh nam là 8%, xong số học sinh nam là số tròn chục có 2 chữ số bé nhất? Đề có vấn đề bạn coi lại nhé. 

ừ bởi mình cũng ko biêt vì bài này là cô mik mà

0,0005=0,05% Bạn nhé

HỌC TỐT

\(\text{0,0005×100=0,05% }\)

pt thứ hai \(\Leftrightarrow\) \(y^2-\left(3x+2\right)y+2x^2+3x+1=0\) (*)

Ta có \(\Delta=\left[-\left(3x+2\right)\right]^2-4\left(2x^2+3x+1\right)\)

\(=9x^2+12x+4-8x^2-12x-4\)

\(=x^2\ge0\) 

Do đó (*) có 2 nghiệm là \(\left[{}\begin{matrix}y=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{3x+2+\sqrt{x^2}}{2}=\dfrac{3x+2+\left|x\right|}{2}\\y=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{3x+2-\sqrt{x^2}}{2}=\dfrac{3x+2-\left|x\right|}{2}\end{matrix}\right.\)

Không mất tính tổng quát, giả sử \(x\ge0\). Khi đó:

\(\left[{}\begin{matrix}y=\dfrac{3x+2+x}{2}=\dfrac{4x+2}{2}=2x+1\\y=\dfrac{3x+2-x}{2}=\dfrac{2x+2}{2}=x+1\end{matrix}\right.\)

Nếu \(y=2x+1\) thì thay vào pt đầu tiên, ta có:

\(x^2+\left(2x+1\right)^2+x+2x+1=8\)

\(\Leftrightarrow5x^2+7x-6=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{5}\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\) \(\Rightarrow y=2x+1=2.\dfrac{3}{5}+1=\dfrac{11}{5}\)

Nếu \(y=x+1\) thì thế vào pt đầu tiên, ta có:

\(x^2+\left(x+1\right)^2+x+x+1=8\)

\(\Leftrightarrow2x^2+4x-6=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-3\left(loại\right)\end{matrix}\right.\) \(\Rightarrow y=x+1=1+1=2\)

 Vậy ta tìm được 2 cặp nghiệm là \(\left(\dfrac{3}{5},\dfrac{11}{5}\right)\) và \(\left(1,2\right)\)

 Tương tự như vậy, xét TH \(x< 0\) thì ta tìm được thêm 2 cặp nghiệm chính là \(\left(-2,-3\right)\) và \(\left(-3,-2\right)\)

phương trình thứ 2 dấu = ở đâu vậy ạ

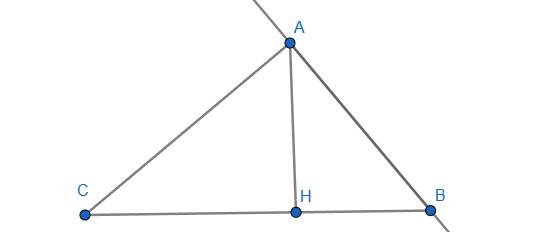
Xét tam giác ABC vuông tại A có AH là đường cao

\(BH.BC=AB^2\)

\(\Rightarrow\left(BC-HC\right)\cdot BC=AB^2\)

\(\Rightarrow\left(BC-19,2\right)\cdot BC=AB^2\)

\(\Rightarrow BC^2-19,2BC=12^2\)

\(\Rightarrow BC^2-19,2BC-144=0\)

\(\Rightarrow BC=\dfrac{48+12\sqrt{41}}{5}\approx24,96\left(cm\right)\)Xét tam giác ABC vuông tại A có

\(BC^2=AB^2+AC^2\)

\(\Rightarrow24,96^2=12^2+AC^2\)

\(\Rightarrow AC\approx21,89\left(cm\right)\)

Xét tam giác ABC vuông tại A có

\(S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}BC.AH\)

\(\Rightarrow\dfrac{1}{2}\cdot12\cdot21,89=\dfrac{1}{2}\cdot24,96\cdot AH\)

\(\Rightarrow AH=\dfrac{262,68}{24,96}\approx10,52\left(cm\right)\)

Vậy độ dài của 𝐴𝐶AC và 𝐴𝐻AH là: 𝐴𝐶≈21,89 cmAC≈21,89cm và 𝐴𝐻≈10,52 cmAH≈10,52cm

Xét ΔABC vuông tại A có AH là đường cao

nên \(AB^2=BH\cdot BC\)

=>\(BH\left(BH+19,2\right)=12^2=144\)

=>\(BH^2+19,2\cdot BH-144=0\)

=>\(\left[{}\begin{matrix}BH=\dfrac{-19,2-\dfrac{24\sqrt{41}}{5}}{2}\left(loại\right)\\BH=\dfrac{-19,2+\dfrac{24\sqrt{41}}{5}}{2}=-9,6+\dfrac{12\sqrt{41}}{5}\left(nhận\right)\end{matrix}\right.\)

=>\(BH=\dfrac{-48+12\sqrt{41}}{5}\)

=>\(BC=\dfrac{-48+12\sqrt{41}}{5}+19,2=\dfrac{48+12\sqrt{41}}{5}\left(cm\right)\)

ΔABC vuông tại A có AH là đường cao

nên \(AH^2=HB\cdot HC=\dfrac{-48+12\sqrt{41}}{5}\cdot19,2=3,84\left(-48+12\sqrt{41}\right)\)

=>\(AH=\sqrt{3,84\left(-48+12\sqrt{41}\right)}\left(cm\right)\)

=>\(AC=\sqrt{AH^2+HC^2}=\sqrt{3,84\left(-48+12\sqrt{41}\right)+19,2^2}\)

=>\(AC=\sqrt{184,32+46,08\sqrt{41}}\)(cm)

Tổng bốn số là:

\(84\times4=336\)

Vì tổng hai số đầu bằng 1/2 tổng 4 số nên tổng số thứ ba và số thứ tư cũng bằng 1/2 tổng 4 số và bằng: \(336:2=168\)

Số thứ ba là:

\(\left(168-16\right):2=76\)

Số thứ tư là:

\(76+16=92\)

a. Diện tích quét sơn là:

\(\left(1,5+0,6\right)\times2\times1,8+1,5\times0,6=8,46\left(m^2\right)\)

b. Nếu đổ đầy thùng nước thì thể tích nước trong thùng là:

\(1,5\times0,6\times1,8=1,62\left(m^3\right)\)

\(\sqrt{x}+\sqrt{2-x}+\sqrt{2x-x^2}=3\) (ĐKXĐ: \(0\le x\le2\))

\(\Leftrightarrow\sqrt{x}+\sqrt{2-x}+\sqrt{x\left(2-x\right)}=3\) (1)

Đặt \(\sqrt{x}+\sqrt{2-x}=a\Rightarrow\dfrac{a^2-2}{2}=\sqrt{x\left(2-x\right)}\) (2) (a > 0)

Thay (2) vào (1), ta được:

\(a+\dfrac{a^2-2}{2}=3\)

\(\Leftrightarrow a^2+2a-2=6\)

\(\Leftrightarrow a^2+2a-8=0\) \(\Leftrightarrow\left[{}\begin{matrix}a=2\\a=-4\end{matrix}\right.\)

Mà a > 0 nên \(a=2\)

\(\Rightarrow\sqrt{x}+\sqrt{2-x}=2\)

\(\Leftrightarrow x+2-x+2\sqrt{x\left(2-x\right)}=2\)

\(\Leftrightarrow2\sqrt{x\left(2-x\right)}=0\)

\(\Leftrightarrow x\left(2-x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\left(tmdk\right)\\x=2\left(tmdk\right)\end{matrix}\right.\)

Vậy ...

a: Để (d) có hệ số góc bằng -2 thì m-1=-2

=>m=-1

b: Thay x=-3 và y=0 vào (d), ta được:

\(-3\left(m-1\right)+2m=0\)

=>-3m+3+2m=0

=>3-m=0

=>m=3

c: Thay x=0 và y=2 vào (d), ta được:

0(m-1)+2m=2

=>2m=2

=>m=1

d: Để (d)//(d1) thì \(\left\{{}\begin{matrix}m-1=-3\\2m\ne4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m=-2\\m\ne2\end{matrix}\right.\)

=>m=-2

a) Tìm 𝑚m để 𝑑d có hệ số góc bằng -2.

Hệ số góc của đường thẳng 𝑑d là 𝑚−1m−1. Để 𝑑d có hệ số góc bằng -2, ta giải phương trình: 𝑚−1=−2

m−1=−2 𝑚=−2+1

\(\Rightarrow\)m=−2+1 𝑚=−1

\(\Rightarrow\)m=−1

b) Tìm 𝑚m để 𝑑d cắt trục hoành tại điểm có hoành độ bằng -3.

Khi 𝑑d cắt trục hoành, 𝑦=0y=0, từ đó: (𝑚−1)𝑥+2𝑚=0

(m−1)x+2m=0 (𝑚−1)(−3)+2𝑚=0

\(\Rightarrow\)(m−1)(−3)+2m=0 3(𝑚−1)+2𝑚=0

\(\Rightarrow\)3(m−1)+2m=0 3𝑚−3+2𝑚=0

\(\Rightarrow\)3m−3+2m=0 5𝑚−3=0

\(\Rightarrow\)5m−3=0 5𝑚=3

\(\Rightarrow\)5m=3 𝑚=35

\(\Rightarrow\)m= 3/5​

c) Tìm 𝑚m để 𝑑d cắt trục tung tại điểm có tung độ bằng 2.

Khi 𝑑d cắt trục tung, 𝑥=0x=0, khi đó: (𝑚−1)⋅0+2𝑚=2

(m−1)⋅0+2m=2

\(\Rightarrow\)2𝑚=2\(\Rightarrow\)2m=2 𝑚=1

\(\Rightarrow\)m=1

d) Tìm 𝑚m để 𝑑d song song với đường thẳng 𝑑1d
​: 𝑦=−3𝑥+4y=−3x+4.

Đường thẳng 𝑑d sẽ song song với 𝑑1d nếu hệ số góc của 𝑑d bằng hệ số góc của 𝑑1d:     dđ𝑚−1=−3

\(\Rightarrow\) m−1=−3 𝑚=−3+1

\(\Rightarrow\)m=−3+1 𝑚=−2

\(\Rightarrow\)m=−2

a) 𝑚=−1m = -1
b) 𝑚=35m = 3/5
​
c) 𝑚=1m = 1
d) 𝑚=−2m = −2

Trung bình cộng 4 số là 84

=> Tổng 4 số là: 84x4=336.

Tổng 2 số đầu =1/2 tổng bốn số

=> Tổng 2 số đầu = Tổng 2 số sau = 336/2=168

Bài toán trở thành tìm 2 số khi biết tổng và hiệu:

Tổng số thứ 3 và thứ 4 = 168

Số thứ 3 kém số thứ tư 16 đơn vị

=> Số thứ 3 = (168-16):2=76

=> Số thứ 4 = 168-76 = 92

Vậy số thứ 3 là 76 và số thứ tư là 92