Bác Hòa mang cam ra chợ,buổi sáng bán được 120 quả,buổi chiều bán được 150 quả.Khi về,bác thấy số cam còn lại bằng 10% tổng số cam ban đầu.Tính số cam ban đầu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có công thức tính thể tích hình lập phương:
V = a x a x a với a là độ dài một cạnh hình lập phương
Nhận thấy: 64 = 4 x 4 x 4
Do đó cạnh hình lập phương bằng 4m
Diện tích tôn để làm hay chính là diện tích toàn phần hình lập phương.
Diện tích tôn cần làm là:
4 x 4 x 6 = 96 (m^2)

Bạn xem lại đề. Kết quả ra $m$ khá xấu, không phù hợp với bài toán PT bậc 2 cơ bản.

16\(\dfrac{10}{13}\) + 3\(\dfrac{3}{13}\) - 8 x 12,5%
= 16 + \(\dfrac{10}{13}\) + 3 + \(\dfrac{3}{13}\) - 1
= (16 + 3) + (\(\dfrac{10}{13}+\dfrac{3}{13}\)) - 1
= 19 + 1 - 1
= 19 + (1 - 1)
= 19
\(16\dfrac{10}{13}+3\dfrac{3}{13}-8x12,5\%\)
=\(20-8x12.5\%\)
=\(20-1=19\)

\(x:0,1-x:0,25\) + \(x:50\%\) = 84,8 + 56
\(x\) x 10 - \(x\) x 4 + \(x\) x 2 = 140,8
\(x\) x (10 - 4 + 2) = 140,8
\(x\) x 8 = 140,8
\(x\) = 140,8 : 8
\(x=17,6\)
x:0,1-x:0,25+x:50%=84,8+56
Xx10-Xx4+Xx2=140,8
Xx(10-4+2)=140,8
Xx8=140.8
X=140.8:8
x=17,6

Bạn nên viết lại đề cho rõ ràng để mọi người đọc hiểu và hỗ trợ nhanh hơn nhé.
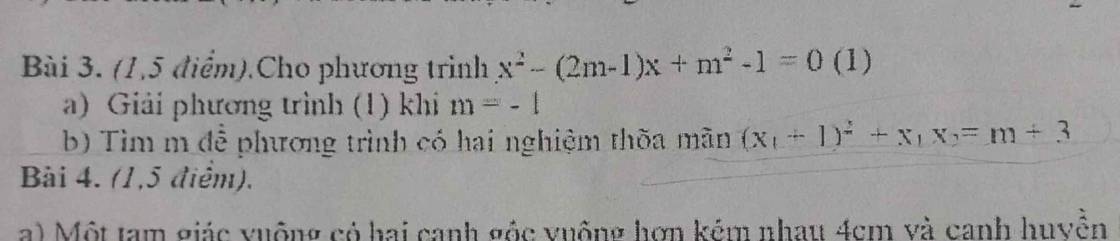
Số cam bán được chiếm số phần trăm tổng số cam ban đầu là:
100% - 10% = 90%
Số cam bán được là:
120 + 150 = 270 (quả)
Số cam ban đầu là:
270 : 90% = 300 (quả)