Cho hình vẽ biết $\widehat{ACB}=40^{\circ};$ $\widehat{BAC}=100^{\circ}$, $Ay$ là tia phân giác của $\widehat{CAx}$.
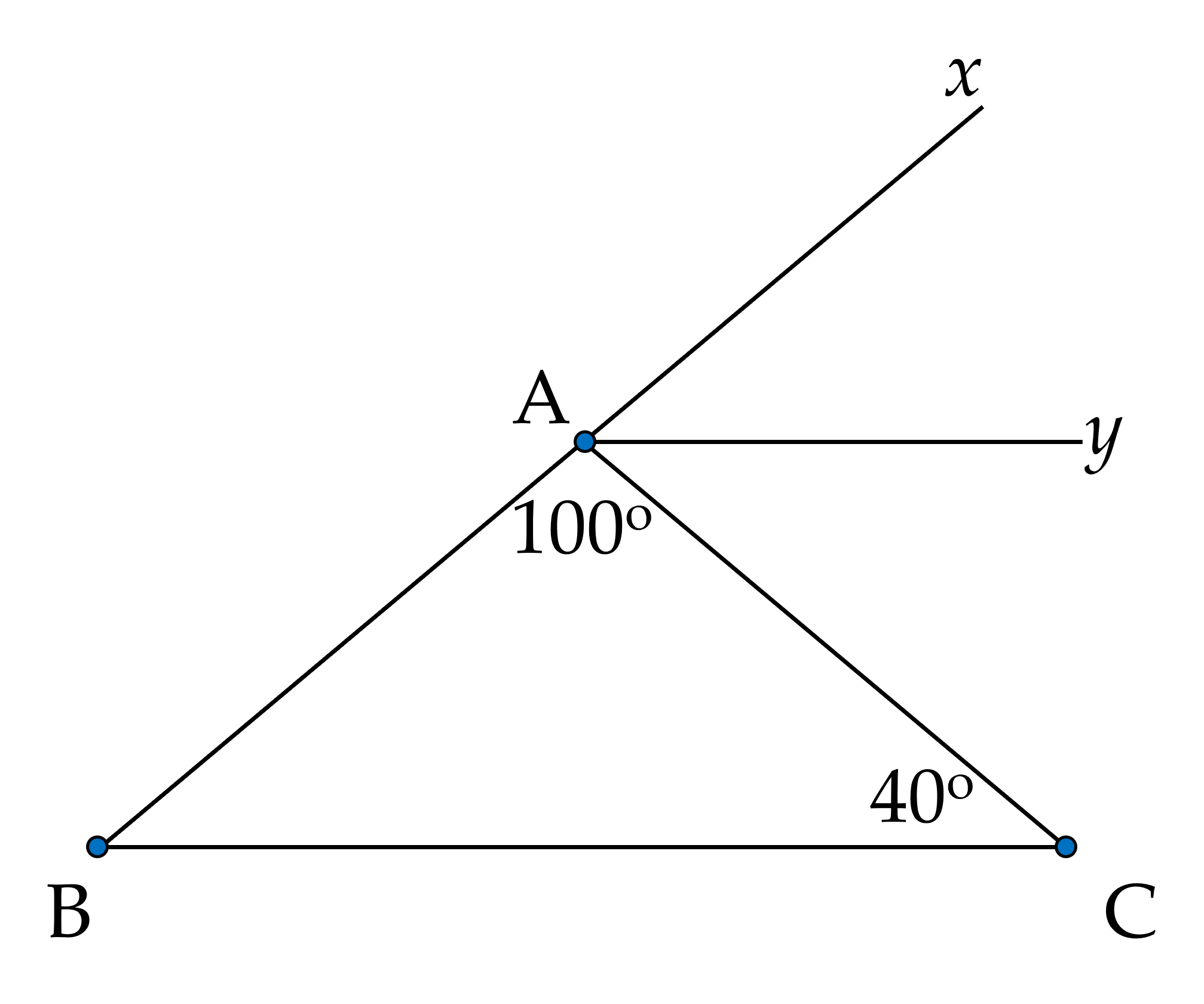
a) Tính $\widehat{CAx}$.
b) Chứng minh $Ay$ // $BC$.
c) Tính số đo $\widehat{ABC}$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,x-\dfrac{2}{3}=\dfrac{1}{6}\\ \Rightarrow x=\dfrac{5}{6}\\ b,2x+\dfrac{1}{2}=-\dfrac{5}{3}\\ \Rightarrow2x=-\dfrac{13}{6}\\ \Rightarrow x=-\dfrac{13}{12}\\ c,3x+\dfrac{3}{2}=x-\dfrac{5}{3}\\ \Rightarrow-4x+\dfrac{3}{2}=-\dfrac{5}{3}\\ \Rightarrow-4x=-\dfrac{19}{6}\\ \Rightarrow4x=\dfrac{19}{6}\\ \Rightarrow x=\dfrac{19}{24}.\)
a) x - 2/3 = 1/6
x = 1/6 + 2/3
x = 5/6
b) 2x + 1/2 = -5/3
2x = -5/3 - 1/2
2x = -13/6
x = -13/6 : 2
x = -13/12
c) 3x + 3/2 = x - 5/3
3x - x = -5/3 - 3/2
2x = -19/6
x = -19/6 : 2
x = -19/12

a) 11/24 - 5/41 + 13/24 + 0,5 - 36/41
= (11/24 + 13/24) - (5/41 + 36/41) + 0,5
= 1 - 1 + 0,5
= 0,5
b) 1/2 . 3/4 + 1/2 . 1/4 + 1/2
= 1/2 . (3/4 + 1/4) + 1/2
= 1/2 . 1 + 1/2
= 1/2 + 1/2
= 1
c) (-3/4)² : (-1/4)² + 9 . (-1/9) + (-3/2)
= 9/16 : 1/16 - 1 - 3/2
= 9 - 1 - 3/2
= 8 - 3/2
= 13/2
d) √0,25 . (-3)³ - √(1/81) : (-1/3)³
= 1/2 . (-27) - 1/9 : (-1/27)
= -27/2 + 3
= -21/2

a) Ta có:
∠mOx + ∠nOx = 180⁰ (kề bù)
⇒ ∠nOx = 180⁰ - ∠mOx
= 180⁰ - 30⁰
= 150⁰
Do Ot là tia phân giác của ∠nOx
⇒ ∠nOt = ∠nOx : 2
= 150⁰ : 2
= 75⁰
b) Do a // b
⇒ ∠B₄ = ∠A₄ = 65⁰ (đồng vị)
Ta có:
∠B₃ + ∠B₄ = 180⁰ (kề bù)
⇒ ∠B₃ = 180⁰ - ∠B₄
= 180⁰ - 65⁰
= 115⁰
Tính số đo góc .
Hướng dẫn giải:a)
Vậy .
là tia phân giác của , suy ra .
b) a // b suy ra (hai góc so le trong).
Mặt khác, ta có
Suy ra .

25% = 1/4
Số đường còn lại sau khi bán 25%:
1 - 1/4 = 3/4 (số đường)
Số đường bán trong ngày thứ hai:
4/9 . 3/4 = 1/3 (số đường)
Số đường ngày thứ ba bán được:
1 - 1/4 - 1/3 = 5/12 (số đường)
Tỉ số đường bán được của ngày thứ ba và ngày thứ nhất:
5/12 : 1/4 = 5/3
Ngày thứ nhất bán được số kg đường là:
(kg đường)
Sau ngày thứ nhất, số đường còn lại là:
(kg)
Ngày thứ hai bán được số kg đường là:
(kg)
Ngày thứ ba bán được số kg đường là:
(kg)
Vậy Ngày thứ 3 bán đc 50kg

a) x + 2/5 = -4/3
x = -4/3 - 2/5
x = -26/15
b) -5/6 + 1/3 x = (-1/2)²
-5/6 + 1/3 x = 1/4
1/3 x = 1/4 + 5/6
1/3 x = 13/12
x = 13/12 : 1/3
x = 13/4
c) 7/12 - (x + 7/6) . 6/5 = (-1/2)³
7/12 - (x + 7/6) . 6/5 = -1/8
(x + 7/6) . 6/5 = 7/12 + 1/8
(x + 7/6) . 6/5 = 17/24
x + 7/6 = 17/24 : 6/5
x + 7/6 = 85/144
x = 85/144 - 7/6
x = -83/144
\(a,x+\dfrac{2}{5}=-\dfrac{4}{3}\\ \Rightarrow x=-\dfrac{26}{15}\\ b,-\dfrac{5}{6}+\dfrac{1}{3}x=\left(-\dfrac{1}{2}\right)^2\\ \Rightarrow-\dfrac{5}{6}+\dfrac{1}{3}x=\dfrac{1}{4}\\ \Rightarrow\dfrac{1}{3}x=\dfrac{13}{12}\\ \Rightarrow x=\dfrac{13}{4}\\ c,\dfrac{7}{12}-\left(x+\dfrac{7}{6}\right).\dfrac{6}{5}=\left(-\dfrac{1}{2}\right)^3\\ \Rightarrow\dfrac{7}{12}-\left(x+\dfrac{7}{6}\right).\dfrac{6}{5}=-\dfrac{1}{8}\\ \Rightarrow\left(x+\dfrac{7}{6}\right).\dfrac{6}{5}=\dfrac{17}{24}\\ \Rightarrow x+\dfrac{7}{6}=\dfrac{85}{144}\\ \Rightarrow x=-\dfrac{83}{144}.\)

a) \(\dfrac{4}{9}+\dfrac{1}{4}=\dfrac{25}{36}\)
b) \(\dfrac{1}{3}\cdot\left(-\dfrac{4}{5}\right)+\dfrac{1}{3}\cdot\left(-\dfrac{1}{5}\right)=\dfrac{1}{3}\cdot\left(-\dfrac{4}{5}-\dfrac{1}{5}\right)=\dfrac{1}{3}\cdot-1=-\dfrac{1}{3}\)
c) \(\dfrac{1}{5}-\left[\dfrac{1}{4}-\left(1-\dfrac{1}{2}\right)^2\right]=\dfrac{1}{5}-\left[\dfrac{1}{4}-\left(\dfrac{1}{2}\right)^2\right]=\dfrac{1}{5}-\left(\dfrac{1}{4}-\dfrac{1}{4}\right)=\dfrac{1}{5}-0=\dfrac{1}{5}\)
`#3107.101107`
`a)`
\(\dfrac{4}{9}+\dfrac{1}{4}=\dfrac{16}{36}+\dfrac{9}{36}=\dfrac{25}{36}\)
`b)`
\(\dfrac{1}{3}\cdot\left(\dfrac{-4}{5}\right)+\dfrac{1}{3}\cdot\left(-\dfrac{1}{5}\right)\)
\(=\dfrac{1}{3}\cdot\left(-\dfrac{4}{5}-\dfrac{1}{5}\right)\)
\(=\dfrac{1}{3}\cdot\left(-1\right)\)
\(=-\dfrac{1}{3}\)
`c)`
\(\dfrac{1}{5}-\left[\dfrac{1}{4}-\left(1-\dfrac{1}{2}\right)^2\right]\)
\(=\dfrac{1}{5}-\left(\dfrac{1}{4}-\dfrac{1}{4}\right)\)
\(=\dfrac{1}{5}-0\)
\(=\dfrac{1}{5}\)

a) Ta có:
∠CAx + ∠CAB = 180⁰ (kề bù)
⇒ ∠CAx = 180⁰ - ∠CAB
= 180⁰ - 100⁰
= 80⁰
b) Do Ay là tia phân giác của ∠CAx
⇒ ∠CAy = ∠xAy = ∠CAx : 2
= 80⁰ : 2
= 40⁰
⇒ ∠CAy = ∠ACB = 40⁰
Mà ∠CAy và ∠ACB là hai góc so le trong
⇒ Ay // BC
c) Do Ay // BC
⇒ ∠ABC = ∠xAy = 40⁰ (đồng vị)