Tìm tập xác định của hàm số f(x)=ln(20-x^2) có bao nhiêu số nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

Tập xác định \(D=ℝ\backslash\left\{2\right\}\)
TCĐ: \(x=2\)
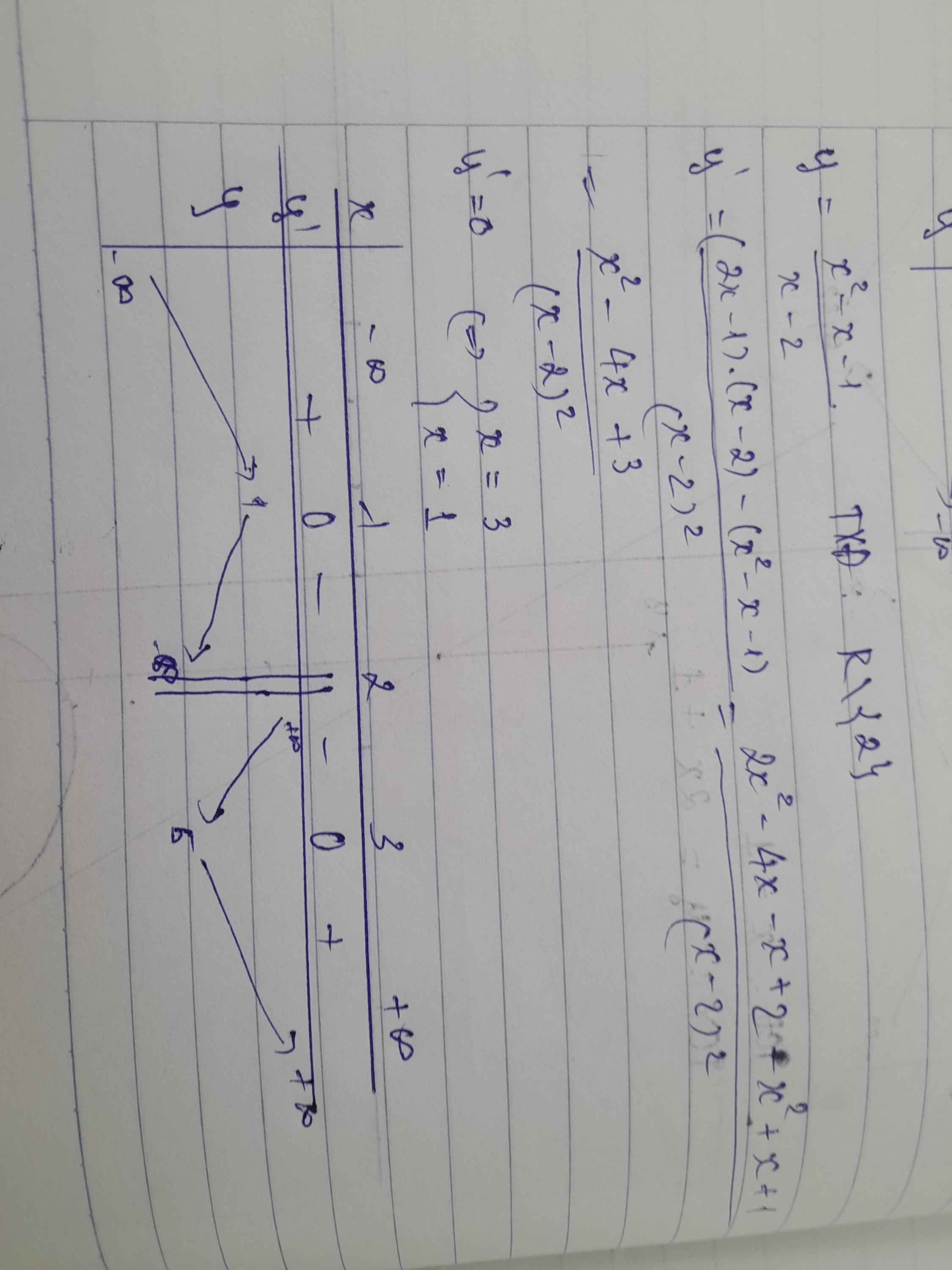
Có \(\dfrac{x^2-x-1}{x-2}=\dfrac{x^2-x-2+1}{x-2}=\dfrac{\left(x+1\right)\left(x-2\right)+1}{x-2}=\left(x+1\right)+\dfrac{1}{x-2}\)
nên đồ thị hàm số có tiệm cận xiên là đường \(y=x+1\)
Có \(y'=\dfrac{x^2-4x+3}{\left(x-2\right)^2}\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
BBT

a) \(y=\dfrac{x+1}{x-2}\)
\(y'=-\dfrac{3}{\left(x-2\right)^2}< 0\forall x\inℝ\ \left\{2\right\}\)
=> hàm số nghịch biến trên \(\left(-\infty;2\right)\) và \(\left(2;+\infty\right)\)
b) \(y=\dfrac{2x+1}{x-1}\)
\(y'=-\dfrac{3}{\left(x-1\right)^2}< 0\forall x\inℝ\ \left\{1\right\}\)
=> hàm số nghịch biến trên \(\left(-\infty;1\right)\) và \((1;+\infty)\)

Kẻ AH\(\perp\)BC tại H, AK\(\perp\)SH tại K
\(\widehat{SB;\left(ABC\right)}=45^0\)
=>\(\widehat{BS;BA}=45^0\)
=>\(\widehat{SBA}=45^0\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}\)
=>\(\dfrac{SA}{a}=tan45=1\)
=>SA=a
ΔABC vuông cân tại A
=>\(AB=AC=a\) và \(BC=\sqrt{AB^2+AC^2}=a\sqrt{2}\)
ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>\(AH=HB=HC=\dfrac{BC}{2}=\dfrac{a\sqrt{2}}{2}\)
Ta có: BC\(\perp\)AH
BC\(\perp\)SA
AH,SA cùng thuộc mp(SAH)
Do đó: BC\(\perp\)(SAH)
=>BC\(\perp\)AK
Ta có: AK\(\perp\)SH
AK\(\perp\)BC
SH,BC cùng thuộc mp(SBC)
Do đó: AK\(\perp\)(SBC)
=>AK là khoảng cách từ A đến mp(SBC)
ΔSAH vuông tại A
=>\(SH^2=SA^2+AH^2=a^2+\left(\dfrac{a\sqrt{2}}{2}\right)^2=a^2+\dfrac{1}{2}a^2=\dfrac{3}{2}a^2\)
=>\(SH=\dfrac{a\sqrt{6}}{2}\)
Xét ΔSAH vuông tại A có AK là đường cao
nên \(AK\cdot SH=SA\cdot AH\)
=>\(AK\cdot\dfrac{a\sqrt{6}}{2}=a\cdot\dfrac{a\sqrt{2}}{2}\)
=>\(AK\cdot\sqrt{6}=a\sqrt{2}\)
=>\(AK=a\sqrt{\dfrac{2}{6}}=a\sqrt{\dfrac{1}{3}}=\dfrac{a\sqrt{3}}{3}\)


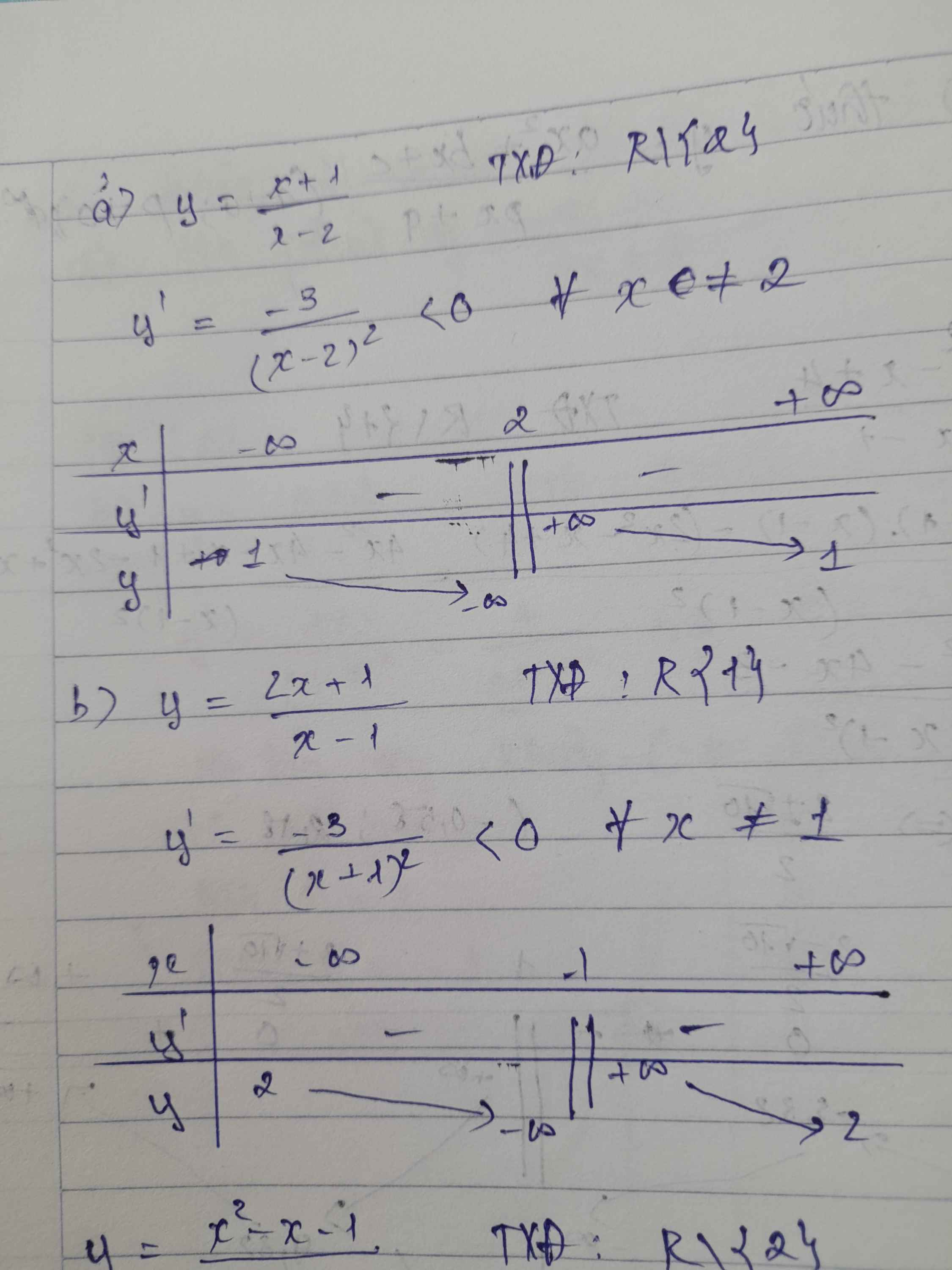



ĐKXĐ: \(20-x^2>0\)
=>\(x^2< 20\)
mà x nguyên
nên \(x\in\left\{0;1;-1;2;-2;3;-3;4;-4\right\}\)
=>Có 9 số nguyên