giải giúp em câu c với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\frac{x\sqrt{y}-y\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
\(=\frac{\left(x\sqrt{y}-y\sqrt{x}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}\)
\(=\frac{\sqrt{xy}.x+xy-xy-\sqrt{xy}.y}{x-y}\)
\(=\frac{\sqrt{xy}.x-\sqrt{xy}.y}{x-y}\)
\(\frac{=\sqrt{xy}.\left(x-y\right)}{x-y}\)
\(=\sqrt{xy}\)


a, \(\sqrt{16x}=8\)ĐK : x >= 0
\(\Leftrightarrow4\sqrt{x}=8\Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\)
c, \(\sqrt{9\left(x-1\right)}=21\Leftrightarrow3\sqrt{x-1}=21\Leftrightarrow\sqrt{x-1}=7\)ĐK : x >= 1
\(\Leftrightarrow x-1=49\Leftrightarrow x=50\)


ĐKXĐ : x \(\ge2\)
Ta có \(\sqrt{x-2}-\sqrt{x+2}=2\sqrt{x^2-4}-2x+2\)
\(\Leftrightarrow\sqrt{x-2}-\sqrt{x+2}=2\sqrt{\left(x-2\right)\left(x+2\right)}-\left(x-2\right)-\left(x+2\right)+2\)
<=> \(\sqrt{x-2}-\sqrt{x+2}=-\left(\sqrt{x-2}-\sqrt{x+2}\right)^2+2\)
Đặt \(\sqrt{x-2}-\sqrt{x+2}=y\)
=> y = -y2 + 2
<=> y2 - y - 2 = 0
<=> (y + 1)(y - 2) = 0
<=> \(\orbr{\begin{cases}y=-1\\y=2\end{cases}}\)
Khi y = -1
<=> \(\sqrt{x-2}-\sqrt{x+2}=-1\)
=> \(\left(\sqrt{x-2}-\sqrt{x+2}\right)^2=1\)
<=> \(\left(x-2\right)+\left(x+2\right)-2\sqrt{\left(x-2\right)\left(x+2\right)}=1\)
<=> \(2x-1=2\sqrt{\left(x-2\right)\left(x+2\right)}\)
=> 4x2 - 4x + 1 = 2(x - 2)(x + 2)
<=> 4x2 - 4x + 1 = 2x2 - 8
<=> 2x2 - 4x + 9 = 0 (vô lý) => TH1 loại
Khi y = 2 =>\(\sqrt{x-2}-\sqrt{x+2}=2\)
=> \(\left(\sqrt{x-2}-\sqrt{x+2}\right)^2=4\)
<=> \(2x-2\sqrt{\left(x-2\right)\left(x+2\right)}=4\)
<=> \(2x-4=2\sqrt{\left(x-2\right)\left(x+2\right)}\)
=> (2x - 4)2 = 4(x - 2)(x + 2)
<=> 4(x - 2)2 = 4(x - 2)(x + 2)
<=> -16(x - 2) = 0
<=> x = 2 (tm)
Vậy x = 2

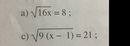
ĐK: \(x\ge0,x\ne1\).
\(A=\frac{x\sqrt{x}+1}{x-1}-\frac{x-1}{\sqrt{x}+1}\)
\(=\frac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}+1}\)
\(=\frac{x-\sqrt{x}+1}{\sqrt{x}-1}-\left(\sqrt{x}-1\right)\)
\(=\frac{x-\sqrt{x}+1-\left(\sqrt{x}-1\right)^2}{\sqrt{x}-1}\)
\(=\frac{x-\sqrt{x}+1-\left(x-2\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=\frac{\sqrt{x}}{\sqrt{x}-1}\)
Với \(x=\frac{9}{4}\):
\(A=\frac{\sqrt{\frac{9}{4}}}{\sqrt{\frac{9}{4}}-1}=\frac{\frac{3}{2}}{\frac{3}{2}-1}=3\)
\(A=\frac{\sqrt{x}}{\sqrt{x}-1}< 1\Leftrightarrow\frac{\sqrt{x}}{\sqrt{x}-1}-1< 0\Leftrightarrow\frac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}-1}< 0\)
\(\Leftrightarrow\frac{1}{\sqrt{x}-1}< 0\)
\(\Leftrightarrow\sqrt{x}-1< 0\)
\(\Leftrightarrow0\le x< 1\).