Lời giải:

a.

$A(x)=-x^5-7x^4-2x^3+x^2+4x+9$

$B(x)=x^5+7x^4+2x^3+2x^2-3x-9$

b. 

$A(x)+B(x)=(-x^5-7x^4-2x^3+x^2+4x+9)+(x^5+7x^4+2x^3+2x^2-3x-9)$

$=(-x^5+x^5)+(-7x^4+7x^4)+(-2x^3+2x^3)+(x^2+2x^2)+(4x-3x)+(9-9)=3x^2+x$

$A(x)-B(x)=(-x^5-7x^4-2x^3+x^2+4x+9)-(x^5+7x^4+2x^3+2x^2-3x-9)$

$=(-x^5-x^5)+(-7x^4-7x^4)+(-2x^3-2x^3)+(x^2-2x^2)+(4x+3x)+(9+9)=-2x^5-14x^4-4x^3-x^2+7x+18$

a, P(x)=(2x^3-x^3)+x^2+(3x-2x)+2=x^3+x^2+x+2
Q(x)=(3x^3-4x^3)+(5x^2-4x^2)+(3x-4x)+1=-x^3+x^2-x+1
b, M(x)=P(x)+Q(x)=x^3+x^2+x+2+(-x^3)+x^2-x+1=2x^2+3
N(x)=P(x)-Q(x)=x^3+x^2+x+2-(-x^3+x^2-x+1)=2x^3+2x+1
c, M(x)=2x^2+3
do x^2>=0 với mọi x=2x^2>=0
nên 2x^2+3>=3 với mọi x
để M(x) có nghiệm thì phải tồn tại x để M(x)=0 ( vô lý vì M(x)>=3 với mọi x)
do đó đa thức M(x) không có nghiệm

`a,A(x)=2x^3+2x-3x^2+11`

`=2x^3-3x^2+2x+11`

`B(x)=2^2+3x^3-x-5`

`=3x^3+2x^2-x-5`

`b, A(x)+B(x)=(2x^3-3x^2+2x+11)+(3x^3+2x^2-x-5)`

`=2x^3-3x^2+2x+11+3x^3+2x^2-x-5`

`=(2x^3+3x^3)+(-3x^2+2x^2)+(2x-x)+(11-5)`

`=5x^3 -x^2 +x+6`

`c,A(x)-B(x)=(2x^3-3x^2+2x+11)-(3x^3+2x^2-x-5)`

`=2x^3-3x^2+2x+11- 3x^3 -2x^2+x+5`

`=(2x^3-3x^3)+(-3x^2-2x^2)+(2x+x)+(11+5)`

`=-x^3 -5x^2+3x+16`

a/\(A\left(x\right)=2x^3+2x-3x^2+11\)
\(=2x^3-3x^2+2x+11\)
\(B\left(x\right)=2x^2+3x^3-x-5\)
\(=3x^3+2x^2-x-5\)
b/\(A\left(x\right)+B\left(x\right)=\left(2x^3-3x^2+2x+11\right)+\left(3x^3+2x^2-x-5\right)\)
\(=2x^3-3x^2+2x+11+3x^3+2x^2-x-5\)
\(=\left(2x^3+3x^3\right)-\left(3x^2-2x^2\right)+\left(2x-x\right)+\left(11-5\right)\)
\(=5x^3-x^2+x+6\)
c/\(A\left(x\right)+B\left(x\right)=\left(2x^3-3x^2+2x+11\right)-\left(3x^3+2x^2-x-5\right)\)
\(=2x^3-3x^2+2x+11-3x^3-2x^2+x+5\)
\(=\left(2x^3-3x^3\right)-\left(3x^2+2x^2\right)+\left(2x+x\right)+\left(11+5\right)\)
\(=-x^3-5x^2+3x+16\)
#DarkPegasus

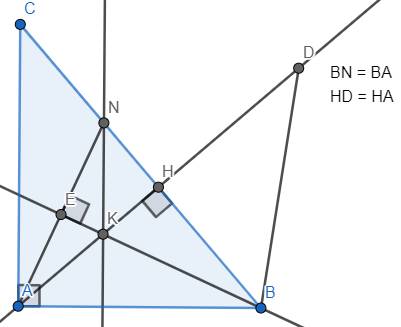
a) Xét ΔABE vuông tại E & ΔNBE vuông tại E có:

- BE là cạnh chung, BN = BA (giả thuyết)

Suy ra ΔABE = ΔNBE (cạnh huyền - cạnh góc vuông)

b) Theo đề ta có BH vuông góc với AD và HA = HD

Suy ra BH là đường trung trực của AD

Suy ra BA = BD (vì B nằm trên đường trung trực của AD)

c) Trong ΔNAB có AH và BE là đường cao, đồng quy tại điểm K

Suy ra NK là đường cao của ΔNAB, hay NK vuông góc với AB

Mà AC cũng vuông góc với AB, suy ra NK // CA

a. - Vì BE vuông góc với AN (gt)
=> tam giác ABE vuông tại E (tc)
     tam giác NBE vuông tại E (tc)
- Xét tam giác vuông ABE và tam giác vuông NBE, có:
    + Chung BE
    + BA = BN (gt)
=> tam giác vuông ABE = tam giác vuông NBE (Cạnh huyền - cạnh  góc vuông)

b. - Vì AH là đường cao của tam giác ABC (gt)
=> tam giác ABH vuông tại H
     tam giác DBH vuông tại H
- Xét tam giác vuông ABH và tam giác vuông DBH, có:
    + Chung BH
    + HA = HD (gt)
=> tam giác vuông ABH = tam giác vuông DBH (2 cạnh góc vuông)
    => BA = BD (2 cạnh tương ứng)

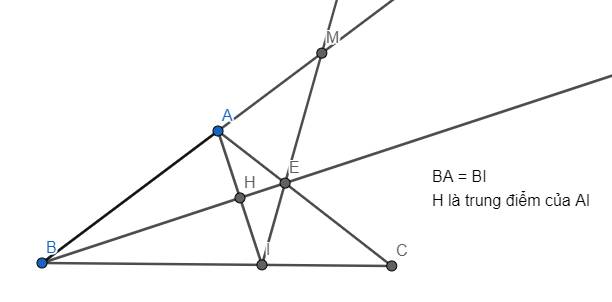
a) Xét ΔABI có:

- BA = BI, suy ra ΔABI cân tại B

- BH là đường trung tuyến đáy AI của ΔABI (do H là trung điểm của AI)

Suy ra BH cũng là đường cao, cũng là đường trung trực của ΔABI.

Khi đó ΔABH & ΔIBH đều vuông tại H. Hai tam giác này có BH là cạnh chung và BA = BI (giả thuyết) nên ΔABH = ΔIBH (cạnh huyền - cạnh góc vuông).

b) Vì BH là đường trung trực của ΔABI (chứng minh trên) và E thuộc BH nên EA = EI. Suy ra ΔAEI cân.

Giúp tôi với

\(\text{A= 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 +...+1/99+1/100}\)

\(A=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)

\(A=1-\dfrac{1}{100}=\dfrac{99}{100}\)

bằng 99/100

Đề không đầy đủ dữ kiện để tính toán. Bạn xem lại

Điều kiện $a,b$ đưa ra chưa rõ ràng. Bạn xem lại.