mảnh đất hình bình hành có cạnh đáy là 47 m, mở rộng mảnh đất bằng cách tăng các cạch đáy của hình bình hành này thêm 7m thì được mảnh đất hình bình hành mới có diện tích hơn diện tích mảnh đất ban đầu là 189m2 .Hãy tính diện tích ban đầu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nếu \(f\left(x\right)=0\) có nghiệm trên \(\left[-1;1\right]\Rightarrow\min\limits_{\left[-1;1\right]}\left[f\left(x\right)\right]^2=0\) ko thỏa mãn yêu cầu
\(\Rightarrow f\left(x\right)=0\) vô nghiệm trên \(\left[-1;1\right]\)
Khi đó
\(f'\left(x\right)=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow f'\left(x\right)\le0;\forall x\in\left[-1;1\right]\)
Xét hàm \(y=\left[f\left(x\right)\right]^2\) trên \(\left[-1;1\right]\)
\(y=\left[f\left(x\right)\right]^2\Rightarrow y'=2f'\left(x\right).f\left(x\right)\)
Do \(f'\left(x\right)\le0\) và \(f\left(x\right)=0\) vô nghiệm (nên ko đổi dấu) trên \(\left[-1;1\right]\) nên:
TH1: \(f\left(x\right)>0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1>-m\)
\(\Rightarrow-m< \min\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=-1\)
\(\Rightarrow m>1\)
Khi đó \(f'\left(x\right).f\left(x\right)\le0\Rightarrow y=\left[f\left(x\right)\right]^2\) nghịch biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(1\right)=\left(1-3+m+1\right)^2=\left(m-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=0< 1\left(loại\right)\\m=2\end{matrix}\right.\)
TH2: \(f\left(x\right)< 0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1< -m\)
\(\Rightarrow-m>\max\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=3\)
\(\Rightarrow m< -3\)
Khi đó \(f'\left(x\right).f\left(x\right)\ge0\Rightarrow y=\left[f\left(x\right)\right]^2\) đồng biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(-1\right)=\left(-1+3+m+1\right)^2=\left(m+3\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=-2>-3\left(loại\right)\\m=-4\end{matrix}\right.\)
Vậy \(m=2;m=-4\) (C đúng)

\(x^3y^4\left(x^2-2y^3\right)-2x^3y^3\left(x^4-y^4\right)\)
\(=x^5y^4-2x^3y^7-2x^7y^3+2x^3y^7\)
\(=x^5y^4-2x^7y^3\)

a: \(\dfrac{3}{7}=\dfrac{3\times5}{7\times5}=\dfrac{15}{35};\dfrac{2}{35}=\dfrac{2}{35};\dfrac{1}{5}=\dfrac{7}{35}\)
Vì 2<7<15
nên trong 1 giờ, vòi 2 chảy được ít nhất, vòi 1 chảy được nhiều nhất
b: Trong 1 giờ, số phần bể nước vòi 1 chảy nhiều hơn vòi 2 là:
\(\dfrac{15}{35}-\dfrac{2}{35}=\dfrac{13}{35}\left(bể\right)\)

Gọi thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình lần lượt là x(giờ) và y(giờ)
(Điều kiện: x>6; y>0)
Người thứ hai hoàn thành công việc nhanh hơn người thứ nhất là 6 giờ nên x-y=6(1)
Trong 1 giờ, người thứ nhất làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, người thứ hai làm được: \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai người làm được: \(\dfrac{1}{4}\)(công việc)
Do đó, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x-y=6\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y+6\\\dfrac{1}{y+6}+\dfrac{1}{y}=\dfrac{1}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{y+y+6}{y^2+6y}=\dfrac{1}{4}\\x=y+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y^2+6y=4\left(2y+6\right)=8y+24\\x=y+6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y^2+6y-8y-24=0\\x=y+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y^2-2y-24=0\\x=y+6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(y-6\right)\left(y+4\right)=0\\x=y+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}y=6\left(nhận\right)\\y=-4\left(loại\right)\end{matrix}\right.\\x=y+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=6\\x=6+6=12\end{matrix}\right.\left(nhận\right)\)
Vậy: thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình lần lượt là 12(giờ) và 6(giờ)

Gọi thời gian làm 1 mình xong việc của người thứ nhất là x giờ, của người thứ hai là y giờ (với x;y>0)
Do người thứ nhất làm 1 mình cần nhiều hơn người thứ hai là 12 giờ nên:
\(x-y=12\) (1)
Trong 1 giờ người thứ nhất làm được \(\dfrac{1}{x}\) phần công việc
Trong 1 giờ người thứ hai làm được \(\dfrac{1}{y}\) phần công việc
Do 2 người làm chung trong 8 giờ xong việc nên:
\(8\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\Rightarrow8x+8y=xy\) (2)
Từ (1) và (2) ta có hệ:
\(\left\{{}\begin{matrix}x-y=12\\8x+8y=xy\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=y+12\\8\left(y+12\right)+8y=y\left(y+12\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=y+12\\y^2-4y-96=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=12\Rightarrow x=24\\y=-8< 0\left(loại\right)\end{matrix}\right.\)

Trong 2 giờ vòi chảy được số lít nước là:
\(900\times2=1800\) (lít)
1800 lít nước chiếm số phần bể là:
\(\dfrac{2}{9}+\dfrac{1}{3}=\dfrac{5}{9}\) (phần bể)
Bể chứa được số lít nước là:
\(1800:\dfrac{5}{9}=3240\) (lít)

Em ghi thế này thì cả C lẫn D đều sai
Đáp án C chắc là \(\widehat{A}=\widehat{C};\widehat{B}=\widehat{D}\) mà em ghi nhầm

`5x^2 (x-y) - 15xy(y-x) `
`= 5x^2 (x-y) + 15xy(x-y) `
`= (5x^2 + 15xy)(x-y) `
`= 5x(x + 3y)(x-y) `
`(x+y)^2 - 6(x+y) + 9` (sửa đề)
`= (x + y - 3)^2 `
`x^2 - 5x + 6`
`= x^2 - 2x - 3x +6`
`= (x^2 - 2x) - (3x - 6) `
`= x(x-2) - 3(x-2) `
`= (x-3)(x-2) `

\(H=2+4+6+...+2024-2.\left(6+12+...+2022\right)\)
\(H=A-2B\) với \(A=2+4+...+2024\) và \(B=6+12+...+2022\)
Số số hạng của A là: \(\left(2024-2\right):2+1=1012\) số
Nên \(A=\left(2+2024\right).1012:2=1025156\)
Số số hạng của B là: \(\left(2022-6\right):6+1=337\) số
Nên \(B=\left(6+2022\right).337:2=341718\)
Vậy \(H=A-2B=341720\)
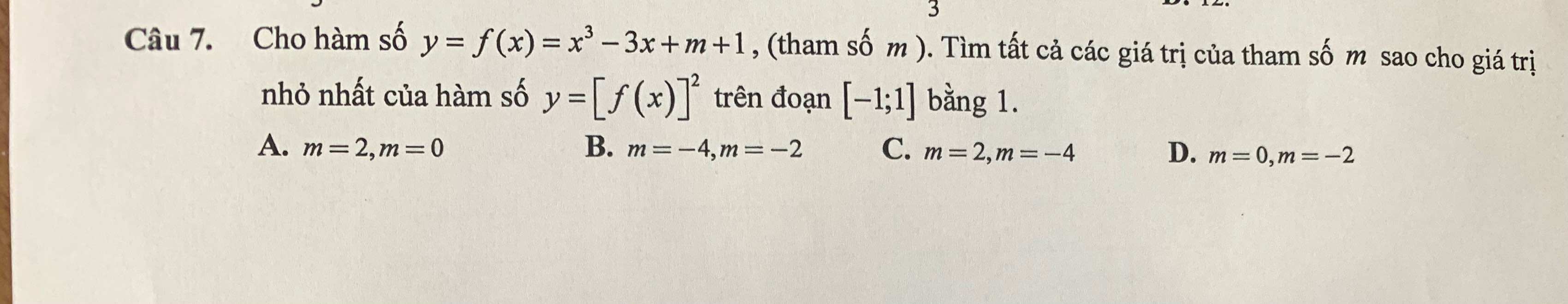
Chiều cao của hình bình hành là:
\(189:7=27\left(m\right)\)
Diện tích ban đầu là \(47\cdot\dfrac{27}{2}=634,5\left(m^2\right)\)
Sau khi mở rộng, cạnh đáy mới là:
\(47+7=54\left(m\right)\)
Chiều cao hình bình hành sau khi tăng là:
\(189:7=27\left(m\right)\)
Diện tích ban đầu là:
\(47\cdot27=1269\left(m^2\right)\)
Đáp số: \(1269m^2\)