phó từ trong cum từ trên là chăm chỉ nhé

phó từ: đã

a) C/m tam giác BAD = tam giác BED

     xét tam giác BAD và tam giác BED, ta có

BD chung

BA = BE (gt)

ABD = DBE (BD tia phân giác góc ABC)

  =>tam giác BAD = tam giác BED

=>AD=DE( cặp cạnh tương ứng)

b) chứng minh AF = EC

Xét tam giác ADF và tam giác EDC, ta có

AD = DE( cmt )

ADF = EDC( đối đỉnh )

DAF=DEC( = 90⁰)

 =>tam giác ADF = tam giác EDC

=>AF = EC ( cặp cạnh tương ứng)

=>ECA=AFE(cặp góc tương ứng )

c)  C/M AE // FC

tam giác BEC có 

BE = BA ( gt )

=> tam giác BEC cân cại B

=>BEA=BAE

ta có

ED = AD

DF = DC

=>ED+DF=AD+DC

=>EF=AC

xét tam giác ACF và tam giác EFC, ta có

EC = AF (cmt)

CF chung

EF=AC(cmt)

=>tam giác ACF= tam giác EFC

=>EFC=ACF(cặp góc tương ứng)

ta có:

ECA = AFE(cmt)

ACF=EFC(cmt)

=>ECA+ACF=AFE+EFC

=>ECF=AFC

tam giác BCF có

BCF=BFC(cmt)

=>tam giác BCF cân tại B

Ta có 

tam giác BEC cân tại B

tam giác BCF cân tại B

=>BEA=BCF=BAE=BFC

mà BEA đồng vị BCF

=> AE//FC

   cái câu c mình ko chắc đúng lắm nha.('v')

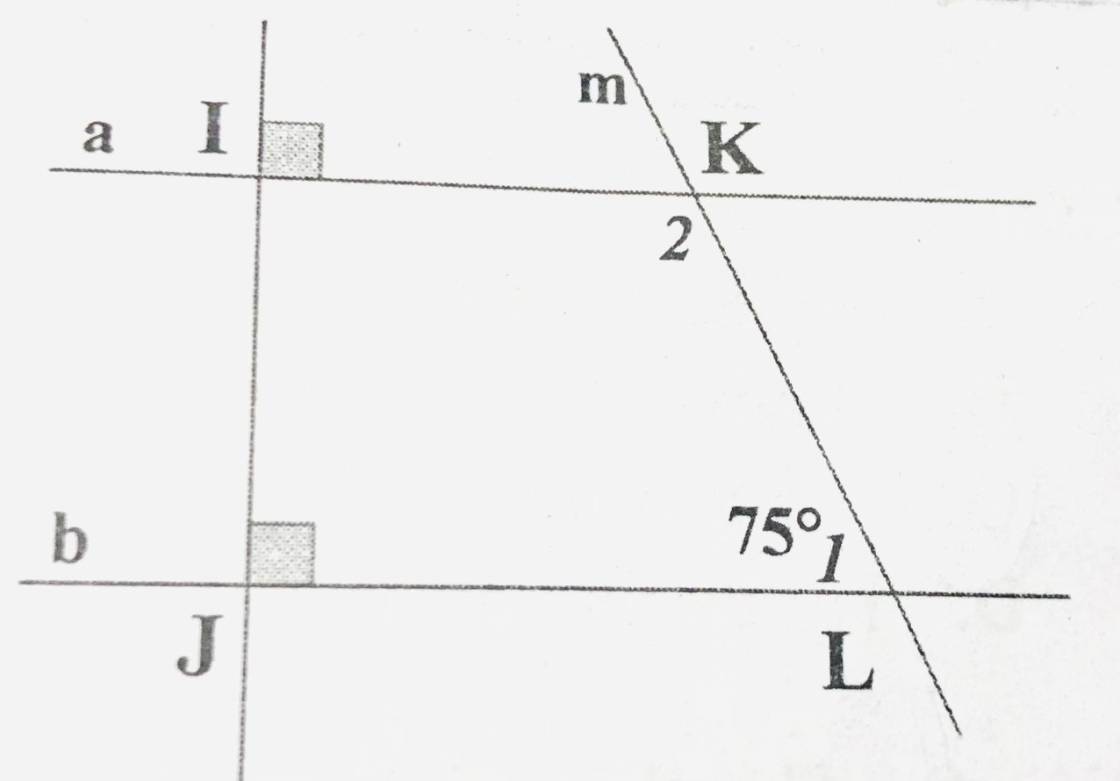
a \(\perp\)  IJ

b  \(\perp\) IJ

⇒ a//b (Vì trong cùng một mặt phẳng hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)

\({}\)\(\widehat{K_2}\) +  \(\widehat{L_1}\)= 180⁰ (hai góc trong cùng phía có tổng bằng 180⁰)

\({}\)  \(\widehat{K_2}\)       = 180⁰ - 75⁰ 

\({}\)   \(\widehat{K_2}\)       = 105⁰ 

Các ký hiệu toán bị lỗi hết rồi bạn. Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.

Ta có: \(\left\{{}\begin{matrix}\left(x+5\right)^2\ge0\forall x\\\left|x-y+1\right|\ge0\forall x,y\end{matrix}\right.\)

\(\Rightarrow\left(x+5\right)^2+\left|x-y+1\right|\ge0\forall x,y\)

\(\Rightarrow-\left[\left(x+5\right)^2+\left|x-y+1\right|\right]\le0\forall x,y\)

\(\Rightarrow-\left(x+5\right)^2-\left|x-y+1\right|\le0\forall x,y\)

\(\Rightarrow P=-\left(x+5\right)^2-\left|x-y+1\right|+2018\le2018\forall x,y\)

Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}x+5=0\\x-y+1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-5\\y=x+1\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=-5\\y=-4\end{matrix}\right.\)

Vậy \(Max_P=2018\) khi \(x=-5;y=-4\).

$Toru$