Ta có: \(\dfrac{x+2y-z}{z}=\dfrac{y+2z-x}{x}=\dfrac{z+2x-y}{y}\left(x,y,z\ne0\right)\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x+2y-z}{z}=\dfrac{y+2z-x}{x}=\dfrac{z+2x-y}{y}\)

\(=\dfrac{x+2y-z+y+2z-x+z+2x-y}{z+x+y}\)

\(=\dfrac{2x+2y+2z}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\)

\(\Rightarrow\dfrac{x+2y-z}{z}=\dfrac{y+2z-x}{x}=\dfrac{z+2x-y}{y}=2\)

\(\Rightarrow\dfrac{x+2y}{z}-1=\dfrac{y+2z}{x}-1=\dfrac{z+2x}{y}-1=2\)

\(\Rightarrow\dfrac{x+2y}{z}=\dfrac{y+2z}{x}=\dfrac{z+2x}{y}=3\)

\(\Rightarrow\dfrac{x+2y}{z}\cdot\dfrac{y+2z}{x}\cdot\dfrac{z+2x}{y}=3\cdot3\cdot3\)

\(\Rightarrow\dfrac{x+2y}{y}\cdot\dfrac{y+2z}{z}\cdot\dfrac{z+2x}{x}=27\)

\(\Rightarrow\left(\dfrac{x}{y}+2\right)\left(\dfrac{y}{z}+2\right)\left(\dfrac{z}{x}+2\right)=27\)

hay \(P=27\)

Vậy: ...

Thanks (´▽`ʃ♡ƪ)

I

1 A

2 D

3 D

4 A

5 D

6 A

7 D

9 A

10 B

11 A

12 D

II

1 does your mother work

2 was eating

3 Did Helen drive - did

4 does - come

5 bought

6 doesn't - water

7 went

8 Did they swim - didn't

9 makes

10 Do children play

11 saw

12 does

13 eat

14 volunteered

Da đầu mỗi người có khoảng 100.000 nang tóc. Một người khỏe mạnh rụng từ 50 – 100 sợi tóc mỗi ngày. Nếu tóc ngày càng mỏng và rụng nhiều hơn bình thường, có thể là dấu hiệu hói đầu.

ai mà biết đc

ik mà đếm tóc trên đầu

a. Ảnh của vật sáng tạo bởi gương phẳng được vẽ đối xứng với vật qua gương phẳng.

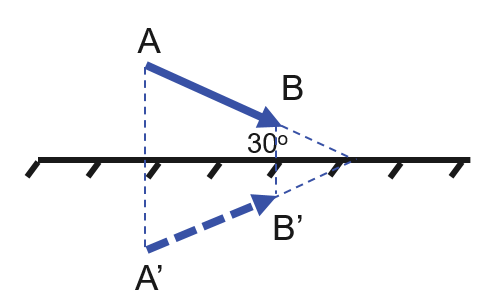
Tính chất của ảnh tạo bởi gương phẳng:

• Ảnh ảo, không hứng được trên màn
• Độ lớn ảnh bằng độ lớn vật
• Khoảng cách từ một điểm của vật đến gương phẳng bằng khoảng cách từ ảnh của điểm đó đến gương

a. Ảnh của vật sáng tạo bởi gương phẳng được vẽ đối xứng với vật qua gương phẳng.

Tính chất của ảnh tạo bởi gương phẳng:

• Ảnh ảo, không hứng được trên màn
• Độ lớn ảnh bằng độ lớn vật
• Khoảng cách từ một điểm của vật đến gương phẳng bằng khoảng cách từ ảnh của điểm đó đến gương

Tốc độ khi lên dốc:

${\text{v}}^1=\genfrac{}{}{0ex}{}{{\text{v}}^2}{2}=\genfrac{}{}{0ex}{}{60}{2}=30$ km/h

Tốc độ khi xuống dốc:

${\text{v}}^3=1,5{\text{v}}^2=1,5.60=90$ km/h

Độ dài cung đường trên là: 

$s=s^1+s^2+s^3={\text{v}}^1{t}^1+{\text{v}}^2{t}^2+{\text{v}}^3{t}^3=30.\genfrac{}{}{0ex}{}{1}{2}+60.\genfrac{}{}{0ex}{}{1}{6}+90.\genfrac{}{}{0ex}{}{1}{6}=40$ km

$t^1$ = 30 min = 1/2  h ; ${\text{v}}^1=\genfrac{}{}{0ex}{}{{\text{v}}^2}{2}$
${\text{v}}^2$ = 60 km/h ; $t^2$ = 10 min = $\genfrac{}{}{0ex}{}{1}{6}$ h 
$t^3$ = 10 min = $\genfrac{}{}{0ex}{}{1}{6}$ h ; ${\text{v}}^3=1,5{\text{v}}^2$
$s$ = ? (km)

Giải:

Tốc độ khi lên dốc:

${\text{v}}^1=\genfrac{}{}{0ex}{}{{\text{v}}^2}{2}=\genfrac{}{}{0ex}{}{60}{2}=30$ km/h

Tốc độ khi xuống dốc:

${\text{v}}^3=1,5{\text{v}}^2=1,5.60=90$ km/h

Độ dài cung đường trên là: 

$s=s^1+s^2+s^3={\text{v}}^1{t}^1+{\text{v}}^2{t}^2+{\text{v}}^3{t}^3=30.\genfrac{}{}{0ex}{}{1}{2}+60.\genfrac{}{}{0ex}{}{1}{6}+90.\genfrac{}{}{0ex}{}{1}{6}=40$ km

Lời giải:
Xét tam giác $OBD$, áp dụng BĐT tam giác thì:

$DB< OB+OD$

Mà $OB=OC$ nên: $OB+OD=OC+OD=CD$

$\Rightarrow DB< CD$ (đpcm)

Hình vẽ:

Lời giải:
a. Ta thấy: $AB\perp BC, CD\perp BC$

$\Rightarrow AB\parallel CD$

$BC\perp CD; DE\perp CD$

$\Rightarrow BC\parallel DE$

b.$AB\perp BC, BC\parallel DE\Rightarrow AB\perp DE$

Mà $DE\perp EF$

$\Rightarrow AB\parallel EF$

c.

Do $AB\parallel CD$ nên: 

$\widehat{AIC}+\widehat{IAB}=180^0$ (2 góc trong cùng phía)

$\Rightarrow \widehat{AIC}=180^0-\widehat{IAB}=180^0-50^0=130^0$