số 2024 là số thứ mấy trong dãy số sau: 2,3,5,8,11,...
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ko tính thời gian nghỉ,thời gian đi là :
75:50=1,5(H)=1h30'
Đến b vào số giờ là :
7H20'+20'+1h30'=9h10'

\(y=x^4-x^2+3\Rightarrow y'=4x^3-2x\)
tung độ là 3 => \(y_0=3\Rightarrow3=x_0^4-x_0^2+3\)\(\Rightarrow x_0=0\)
\(y'\left(x_0\right)=0^4-0^2=3=3\)
=> phương trình tiếp tuyến: \(y=y'\left(x_0\right)\left(x-x_0\right)+y_0\)
=> y=3(x-0)+3=3x+3

1: Xét ΔEBA vuông tại B và ΔEDF vuông tại D có
\(\widehat{BEA}\) chung
Do đó: ΔEBA~ΔEDF
2: Xét ΔIDA vuông tại D và ΔIBF vuông tại B có
\(\widehat{DIA}=\widehat{BIF}\)(hai góc đối đỉnh)
Do đó: ΔIDA~ΔIBF
=>\(\dfrac{ID}{IB}=\dfrac{IA}{IF}\)
=>\(ID\cdot IF=IA\cdot IB\)

1: 7-(x-3)=2(3-4x)
=>7-x+3=6-8x
=>-x+10=6-8x
=>-x+8x=6-10
=>7x=-4
=>\(x=-\dfrac{4}{7}\)
2: ĐKXĐ: \(x\notin\left\{1;3\right\}\)
\(\dfrac{3x}{x-1}=\dfrac{2x}{x-3}-\dfrac{4x}{\left(x-1\right)\left(x-3\right)}\)
=>\(\dfrac{3x\left(x-3\right)}{\left(x-1\right)\left(x-3\right)}=\dfrac{2x\left(x-1\right)}{\left(x-3\right)\left(x-1\right)}-\dfrac{4x}{\left(x-1\right)\left(x-3\right)}\)
=>\(3x^2-9x=2x^2-2x-4x\)
=>\(3x^2-9x=2x^2-6x\)
=>\(x^2-3x=0\)
=>x(x-3)=0
=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=3\left(loại\right)\end{matrix}\right.\)
3: \(2\left(3x+1\right)-3\left(5x+2\right)>2x-9\)
=>6x+2-15x-6>2x-9
=>-9x-4>2x-9
=>-11x>-5
=>\(x< \dfrac{5}{11}\)

1: |2x-1|=3
=>\(\left[{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}2x=4\\2x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(loại\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)
Thay x=-1 vào A, ta được:
\(A=\dfrac{-1-1}{\left(-1\right)^2-4}=\dfrac{-2}{1-4}=\dfrac{-2}{-3}=\dfrac{2}{3}\)
2: \(B=\dfrac{x-3}{x-2}-\dfrac{3}{x+2}-\dfrac{4x+5}{4-x^2}\)
\(=\dfrac{x-3}{x-2}-\dfrac{3}{x+2}+\dfrac{4x+5}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{\left(x-3\right)\left(x+2\right)-3\left(x-2\right)+4x+5}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2-x-6-3x+6+4x+5}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+5}{x^2-4}\)
3: \(\dfrac{A}{B}< 0\)
=>\(\dfrac{x-1}{x^2-4}:\dfrac{x^2+5}{x^2-4}< 0\)
=>\(\dfrac{x-1}{x^2+5}< 0\)
=>x-1<0
=>x<1
Kết hợp ĐKXĐ, ta được:
\(\left\{{}\begin{matrix}x< 1\\x\ne-2\end{matrix}\right.\)

\(\dfrac{1}{2}-\left(-\dfrac{2}{5}\right)+\dfrac{1}{3}+\dfrac{5}{7}-\left(-\dfrac{1}{6}\right)+\left(-\dfrac{4}{35}\right)+\dfrac{1}{41}\)
\(=\dfrac{1}{2}+\dfrac{2}{5}+\dfrac{1}{3}+\dfrac{5}{7}+\dfrac{1}{6}+-\dfrac{4}{35}+\dfrac{1}{41}\)
\(=\left(\dfrac{1}{2}+\dfrac{1}{6}\right)+\left(\dfrac{2}{5}+-\dfrac{4}{35}+\dfrac{5}{7}\right)+\dfrac{1}{41}+\dfrac{1}{3}\)
\(=\dfrac{2}{3}+1+\dfrac{1}{3}+\dfrac{1}{41}\)
\(=\left(\dfrac{2}{3}+\dfrac{1}{3}\right)+1+\dfrac{1}{41}\)
\(=1+1+\dfrac{1}{41}\)
\(=2+\dfrac{1}{41}\)
\(=\dfrac{83}{41}\)
\(#GP\)

\(a,M\left(x\right)=A\left(x\right)-2\cdot B\left(x\right)+C\left(x\right)\\ =\left(2x^5-4x^3+x^2-2x+2\right)-2\left(x^5-2x^4+x^2-5x+2\right)+\left(x^4+4x^3+3x^2-8x+2\dfrac{3}{4}\right)\\ =2x^5-4x^3+x^2-2x+2-2x^5+4x^4-2x^2+10x-4+x^4+4x^3+3x^2-8x+2,75\\ =\left(2x^5-2x^5\right)+\left(4x^4+x^4\right)+\left(-4x^3+4x^3\right)+\left(x^2-2x^2+3x^2\right)+\left(-2x+10x-8x\right)+\left(2-4+2,75\right)\\ =5x^4+2x^2+0,75\)
b, Thay x = -√0,25 = -0,5 vào M(x)
\(M\left(-0,5\right)=5\cdot\left(-0,5\right)^4+2\cdot\left(-0,5\right)^2+0,75\\ =0,3125+0,5+0,75\\ =1,5625\)
c, Vì \(5x^4\ge0;2x^2\ge0=>M\left(x\right)\ge0,75\)
Vậy không có giá trị nào của x để M(x) = 0


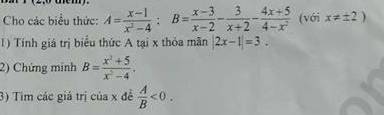
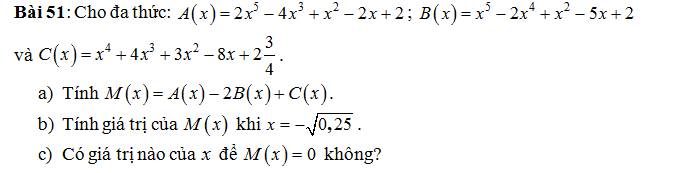
mình ko chắc nhé!
2026 nhé!!
2025 nhé vừa nãy mình tính sai nhé mình cũng ko chắc đâu sai thì bạn thông cảm nhé