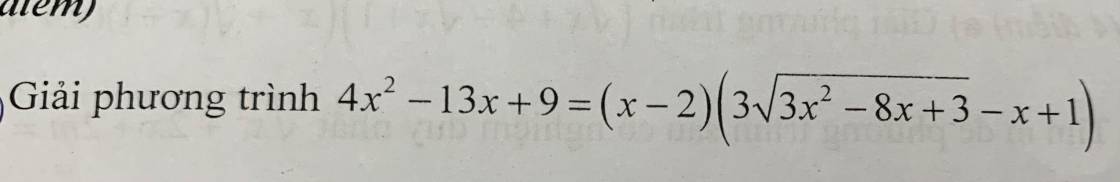Gọi số cần lập là \(\overline{abcd}\)

a có 4 cách chọn (khác 0), b có 4 cách chọn (khác a), c có 3 cách chọn (khác a,b), d có 2 cách chọn

\(\Rightarrow\) Có \(4.4.3.2=96\) số

\(\sqrt{x^2-x-1}=\sqrt{x-1}\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-1\ge0\\x^2-x-1=x-1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x^2-2x=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\end{matrix}\right.\)

\(\Rightarrow x=2\)

bài này đi thi toán nâng cao lớp 5 cũng có dạng như này

giải nhanh dùm e ạ

 Số cách chọn 5 trong số 12 cuốn sách là \(C^5_{12}\)

 Ta đi tính số cách chọn 5 trong 12 cuốn sách sao cho không có cả 3 loại sách trong số sách còn lại.

 TH1: Chọn 5 quyển sách toán \(\Rightarrow\) Có 1 cách.

 TH2: Chọn 4 quyển sách văn và 1 quyển sách khác \(\Rightarrow\) Có 8 cách.

 TH3: Chọn 3 quyển sách anh và 2 quyển sách khác \(\Rightarrow\) Có \(C^2_9=36\) cách.

Vậy có tất cả \(1+8+36=45\) cách chọn 5 quyển sách sao cho trong số sách còn lại không chứa cả 3 loại sách.

 \(\Rightarrow\) Có \(C^5_{12}-45=747\) cách chọn thỏa mãn ycbt.

A(-1;1); B(1;3); C(1;-1)

\(AB=\sqrt{\left(1+1\right)^2+\left(3-1\right)^2}=2\sqrt{2}\)

\(AC=\sqrt{\left(1+1\right)^2+\left(-1-1\right)^2}=\sqrt{2^2+2^2}=2\sqrt{2}\)

\(BC=\sqrt{\left(1-1\right)^2+\left(-1-3\right)^2}=4\)

Chu vi tam giác ABC là: 

\(AB+AC+BC=2\sqrt{2}+2\sqrt{2}+4=4\sqrt{2}+4\)

Xét ΔABC có \(AB^2+AC^2=BC^2\)

nên ΔABC vuông tại A

Xét ΔABC vuông tại A có AB=AC

nên ΔABC vuông cân tại A

=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot2\sqrt{2}\cdot2\sqrt{2}=4\)

a) Ta có \(AB^2=\left[\left(-3\right)-\left(-1\right)\right]^2+\left(5-3\right)^2=8\)

Do đó pt đường tròn \(\left(A,AB\right):\left(x+1\right)^2+\left(y-3\right)^2=8\)

b) Pt đường thẳng AB có dạng:

 \(AB:\dfrac{y-3}{5-3}=\dfrac{x+1}{-3+1}\) 

\(\Leftrightarrow\dfrac{y-3}{2}=\dfrac{x+1}{-2}\) 

\(\Leftrightarrow y-3=-x-1\) 

\(\Leftrightarrow x+y-2=0\)

1) Gọi các số thỏa mãn là \(\overline{abcdef}\)

Số cách chọn vị trí của 3 chữ số 2 là \(C^3_6\)

Số cách chọn vị trí của 2 chữ số 1 là \(C^2_3\)

Số cách chọn 2 chữ số còn lại: \(4^2\)

\(\Rightarrow\) Có tất cả \(C^3_6.C^2_3.4^2=960\) số thỏa ycbt

2) Tập con X bất kì của A muốn thỏa mãn ycbt thì đk cần là phải có ít nhất 1 và nhiều nhất 7 phần tử.

 TH1: \(X=\left\{2\right\}\) -> Có 1 tập X

 TH2: \(X=\left\{2;a_1\right\}\) -> Có \(C^1_6\) tập X

 TH3: \(X=\left\{2;a_1;a_2\right\}\) -> Có \(C^2_6\) tập X

 ...

 TH7: \(X=\left\{2;a_1;...;a_6\right\}\) -> Có \(C^6_6\) tập X

 \(\Rightarrow\) Có tất cả \(1+C^1_6+C^2_6+...+C^6_6=2^6=32\) tập hợp thỏa ycbt.

3) Gọi số thỏa mãn ycbt là \(\overline{abcde}\)

Số cách chọn 2 vị trí của 2 chữ số lẻ liền nhau là 3 cách.

TH1: \(a,b\) lẻ thì có \(P^2_3=6\) cách chọn cặp \(\left(a;b\right)\), bộ \(\left(c;d;e\right)\) có \(P^3_4=24\) cách chọn => Có \(6.24=144\) số

TH2: \(b,c\) lẻ thì cũng có \(P^2_3=6\) cách chọn cặp \(\left(b;c\right)\), còn bộ \(\left(a;d;e\right)\) có \(3.3.2=18\) cách chọn => Có \(6.18=108\) số

TH3: \(c,d\) lẻ thì tương tự TH2, có 108 số.

\(\Rightarrow\) Có tất cả \(144+108+108=360\) số thỏa mãn ycbt.

Lời giải:
PT $\Leftrightarrow 5x^2-16x+11=3(x-2)\sqrt{3x^2-8x+3}$
Đặt $x-2=a; \sqrt{3x^2-8x+3}=b(b\geq 0)$
Khi đó:
$2a^2+b^2=2(x-2)^2+(3x^2-8x+3)=5x^2-16x+11$
PT đã cho trở thành:
$2a^2+b^2=3ab$

$\Leftrightarrow 2a^2+b^2-3ab=0$

$\Leftrightarrow (a-b)(2a-b)=0$

$\Leftrightarrow a=b$ hoặc $2a=b$

Nếu $a=b$

$\Leftrightarrow x-2=\sqrt{3x^2-8x+3}$

$\Leftrightarrow (x-2)^2=3x^2-8x+3$ ($x\geq 2$)

$\Leftrightarrow 2x^2-4x-1=0$

$\Leftrightarrow x=\frac{2\pm \sqrt{6}}{2}$

Do $x\geq 2$ nên $x=\frac{2+\sqrt{6}}{2}$

Nếu $2a=b$

$\Leftrightarrow 2(x-2)=\sqrt{3x^2-8x+3}$

$\Leftrightarrow 4(x-2)^2=3x^2-8x+3$ ($x\geq 2$)

$\Leftrightarrow x^2-8x+13=0$

$\Leftrightarrow x=4\pm \sqrt{3}$