Lời giải:
a. Xét tam giác $AHB$ và $CAB$ có:
$\widehat{AHB}=\widehat{CAB}=90^0$

$\widehat{B}$ chung

$\Rightarrow \triangle AHB\sim \triangle CAB$ (g.g)

b. Từ tam giác đồng dạng phần a suy ra:

$\frac{HB}{AB}=\frac{AB}{CB}$

$\Rightarrow HB=\frac{AB^2}{BC}=\frac{AB^2}{\sqrt{AB^2+AC^2}}=\frac{15^2}{\sqrt{15^2+20^2}}=9$ (cm)

c. Xét tam giác $AHD$ và $ABH$ có:

$\widehat{A}$ chung

$\widehat{ADH}=\widehat{AHB}=90^0$

$\Righarrow \triangle AHD\sim \triangle ABH$ (g.g)

$\Rightarrow \frac{AH}{AB}=\frac{AD}{AH}$

$\Rightarrow AB.AD=AH^2(*)$

Tương tự ta cũng chỉ ra $\triangle AHE\sim \triangle ACH$ (g.g)

$\Rightarrow AE.AC=AH^2(**)$
Từ $(*); (**)\Rightarrow AB.AD=AE.AC$ (đpcm)

Hình vẽ:

Chưa ai giúp em hả olm tới rồi em nhé.

=> Thắng \(\times\) 2 > Nam \(\times\) 2 

=> Thắng > Nam > Việt + Chiến ( 1)

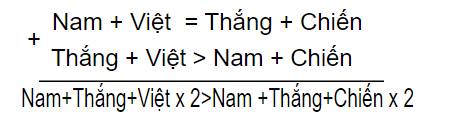
=> Việt > Chiến   (2) 

Kết hợp (1)  và (2) ta có : Thắng > Nam > Việt > Chiến

Vậy Thắng thứ nhất; Nam thứ hai; Việt thứ ba và Chiến thứ tư

Ghi nhớ : Muốn tính Chiều dài của một vật mà đoàn tàu vượt qua, ta cần tính độ dài quãng đường mà tàu đi được trong thời gian vượt qua vật đó rồi trừ đi chiều dài đoàn tầu.

Đổi: 8 phút + 12 giây = \(\dfrac{8}{60}\) giờ + \(\dfrac{12}{3600}\) giờ = \(\dfrac{41}{300}\) giờ

Quãng đường mà đoàn tàu đi được trong thời gian 8 phút 12 giây là:

               48 \(\times\) \(\dfrac{41}{300}\) = 6,56 (km)

         Đổi 6,56 km = 6560 m

Đường hầm đó dài : 6560 - 120 = 6440 (m)

Đáp số:  6440 m 

\(M=6x^2+4y^2+6xy+\left(xy+\dfrac{4x}{y}\right)+\left(3xy+\dfrac{3y}{x}\right)+2022\)

\(M\ge3x^2+y^2+3\left(x+y\right)^2+2\sqrt{\dfrac{4x^2y}{y}}+2\sqrt{\dfrac{9xy^2}{x}}+2022\)

\(M\ge3\left(x^2+1\right)+\left(y^2+4\right)+3\left(x+y\right)^2+4x+6y+2015\)

\(M\ge6x+4y+3\left(x+y\right)^2+4x+6y+2015\)

\(M\ge3\left(x+y\right)^2+10\left(x+y\right)+2015\ge3.3^2+10.3+2015=2072\)

Dấu "=" xảy ra khi \(\left(x;y\right)=\left(1;2\right)\)

Tỉ số biểu thị số cây của 2 tổ là:

\(\dfrac{Tổ1}{Tổ2}=\dfrac{3}{4}\)

Tổng số phần bằng nhau là: 3 + 4 = 7 (phần)

Số cây tổ 1 trồng được là: 105 : 7 x 3 = 45 (cây)

Số cây tổ 2 trồng được là: 105 : 7 x 4 = 60  (cây)

Đáp số: Tổ 1: 45 cây

              Tổ 2: 60 cây

D

A. 100 cm2

4 x 5²=100

Đáp án A