-5/6 - x = 7/12 + -1/3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\dfrac{5}{24}=\dfrac{5.7}{24.7}=\dfrac{35}{168};\dfrac{-21}{56}=\dfrac{-21.3}{56.3}=\dfrac{-63}{168}\\ b,\dfrac{-21}{51}=\dfrac{-21:3}{51:3}=\dfrac{-7}{17}=\dfrac{-7.16}{17.16}=\dfrac{-112}{272};\dfrac{-3}{16}=\dfrac{-3.17}{17.16}=\dfrac{-51}{272}\)
a) 5/24 = 35/168
-21/56 = -63/168
b) -3/16 = -48/272
-21/51 = -7/17 = -112/272

Dãy số các số tự nhiên có 5 chữ số là:
\(10000;10001;10002;10003;...;99999\)
Khoảng cách của 2 số liên tiếp cách nhau:
\(1-0=1\)
Số số hạng của dãy số các số tự nhiên có 5 chữ số là:
\(\left(99999-10001\right):1+1=89999\left(số\right)\)
Đáp số: \(89999\) số.

\(D=\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)...\left(1-\dfrac{1}{99^2}\right)\)
\(D=\dfrac{2^2-1}{2^2}\cdot\dfrac{3^2-1}{3^2}...\cdot\dfrac{99^2-1}{99^2}\)
\(D=\dfrac{\left(2+1\right)\left(2-1\right)}{2^2}\cdot\dfrac{\left(3+1\right)\left(3-1\right)}{3^2}\cdot...\cdot\dfrac{\left(99+1\right)\left(99-1\right)}{99^2}\)
\(D=\dfrac{3\cdot1}{2^2}\cdot\dfrac{4\cdot2}{3^2}\cdot\dfrac{5\cdot3}{4^2}\cdot\dfrac{6\cdot4}{5^2}\cdot...\cdot\dfrac{100\cdot98}{99^2}\)
\(D=\dfrac{1\cdot2\cdot3^2\cdot4^2\cdot5^2\cdot6^2\cdot...\cdot98^2\cdot99\cdot100}{2^2\cdot3^2\cdot...\cdot99^2}\)
\(D=\dfrac{2\cdot99\cdot100}{2^2\cdot99^2}\)
\(D=\dfrac{100}{2\cdot99}\)
\(D=\dfrac{50}{99}\)

4.
\(\dfrac{x-7}{y-6}=\dfrac{7}{6}\Rightarrow\dfrac{x-7}{7}=\dfrac{y-6}{6}=\dfrac{-y+6}{-6}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x-7}{7}=\dfrac{-y+6}{-6}=\dfrac{x-7-y+6}{7-6}=\dfrac{x-y-1}{1}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}x-7=7.\left(-5\right)=-35\\-y+6=\left(-6\right).\left(-5\right)=30\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-28\\y=-24\end{matrix}\right.\)
5.
Ta có:
\(A^2=\dfrac{2^2.4^2.6^2...4998^2.5000^2}{3^2.5^2.7^2...4999^2.5001^2}< \dfrac{2^2.4^2.6^2.4998^2.5000^2}{\left(3^2-1\right)\left(5^2-1\right)\left(7^2-1\right)...\left(4999^2-1\right)\left(5001^2-1\right)}\)
\(\Rightarrow A^2< \dfrac{2^2.4^4.6^2...4998^2.5000^2}{2.4.4.6.6.8...4998.5000.5000.5002}=\dfrac{2^2.4^4.6^2...4998^2.5000^2}{2.4^4.6^2...4998^2.5000^2.5002}\)
\(\Rightarrow A^2< \dfrac{2}{5002}=\dfrac{1}{2501}< \dfrac{1}{2500}\)
\(\Rightarrow A< \dfrac{1}{50}\)
\(\Rightarrow A< 0,02\)
Bài 3:
\(A=B\) khi:
\(\dfrac{7}{y-2}=x+1\left(y\ne2\right)\)
\(\Rightarrow\left(x+1\right)\left(y-2\right)=7\)
Mà: x,y nguyên \(\Rightarrow x+1,y-2\inƯ\left(7\right)=\left\{1;-1;7;-7\right\}\)
Ta có bảng sau:
| x + 1 | 1 | -1 | 7 | -7 |
| y - 2 | 7 | -7 | 1 | -1 |
| x | 0 | -2 | 6 | -8 |
| y | 9 | -5 | 3 | 1 |

\(M=\dfrac{10-3n}{5-3n}=\dfrac{5+5-3n}{5-3n}=\dfrac{5}{5-3n}+1\)
\(M\in Z\Rightarrow\dfrac{5}{5-3n}\in Z\)
\(\Rightarrow5-3n=Ư\left(5\right)=\left\{-5;-1;1;5\right\}\)
\(\Rightarrow\left[{}\begin{matrix}5-3n=-5\Rightarrow n=\dfrac{10}{3}\notin Z\left(loại\right)\\5-3n=-1\Rightarrow n=2\\5-3n=1\Rightarrow n=\dfrac{4}{3}\notin Z\left(loại\right)\\5-3n=5\Rightarrow n=0\end{matrix}\right.\)
Vậy \(n=\left\{0;2\right\}\)

Ta có: \(10^8=\overline{10...0}\) (8 số 0)
\(10^8+8=\overline{10...8}\)
Vậy chữ số tận cùng là 8


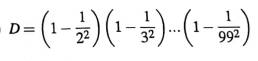


\(-\dfrac{5}{6}-x=\dfrac{7}{12}+\left(-\dfrac{1}{3}\right)\\ -\dfrac{5}{6}-x=\dfrac{7}{12}-\dfrac{1}{3}=\dfrac{7-1.4}{12}=\dfrac{3}{12}=\dfrac{1}{4}\\ x=-\dfrac{5}{6}-\dfrac{1}{4}=\dfrac{-5.2-1.3}{12}=\dfrac{-13}{12}\)