tìm giá trị nhỏ nhất của biểu thức:
A=(2x-1)4+3
B=-(8x-\(\dfrac{4}{5}\))6+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


S \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{9.10}\)
\(S=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
\(S=1-\dfrac{1}{10}\)
\(S=\dfrac{9}{10}\)
N= \(\dfrac{1}{9.11}+\dfrac{1}{11.13}+\dfrac{1}{13.15}+\dfrac{1}{15.16}+...+\dfrac{1}{43.47}\)
N= \(\dfrac{1}{2}.\left(\dfrac{2}{9.11}+\dfrac{2}{11.13}+\dfrac{2}{13.15}+...+\dfrac{2}{43.45}\right)\)
N= \(\dfrac{1}{2}.\left(\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{15}+...+\dfrac{1}{43}-\dfrac{1}{45}\right)\)
N= \(\dfrac{1}{2}.\left(\dfrac{1}{9}-\dfrac{1}{45}\right)\)
N=\(\dfrac{1}{2}\) . \(\dfrac{4}{45}\)
N= \(\dfrac{2}{45}\)

a,\(-\left(m+n-k\right)+\left(m-k\right)-\left(-m+n\right)\\ =-m-n+k+m-k+m-n\\ =m-2n\)
b, \(\left(x-y\right)-\left(x+y\right)-\left(2x-3y\right)\\ =x-y-x-y-2x+3y\\ =-2x+y\)

Gọi đường chéo của hình thoi là d và chu vi đáy là p.
Ta có hệ phương trình sau:
d + d = 24cm (vì đường chéo của hình thoi bằng 24cm)
p = 52cm (vì chu vi đáy của hình thoi bằng 52cm)
Từ đó, ta có:
2d = 24cm
d = 12cm
Vậy đường chéo của hình thoi là 12cm.
Để tính chiều cao của hình lăng trụ, ta sử dụng định lý Pytago:
Chiều cao của hình lăng trụ = căn bậc hai của (d^2 - (cạnh đáy/2)^2)
= căn bậc hai của (12^2 - (10/2)^2)
= căn bậc hai của (144 - 25)
= căn bậc hai của 119
≈ 10.92cm
Vậy chiều cao của hình lăng trụ là khoảng 10.92cm.
Để tính thể tích của hình lăng trụ, ta sử dụng công thức:
Thể tích = diện tích đáy x chiều cao
= (diện tích hình thoi x 2) x chiều cao
= (cạnh đáy x cạnh đáy x sin(góc giữa hai đường chéo) x 2) x chiều cao
= (10cm x 10cm x sin(90°) x 2) x 10.92cm
= (100cm^2 x 1 x 2) x 10.92cm
= 2184cm^3
Vậy thể tích của hình lăng trụ là 2184cm^3

\(0,4^4=\left(0,04.10\right)^4=0,2^8.10^4\)
\(0,8^3=\left(0,008.100\right)^3=0,2^9.10^5>0,2^8.10^4\)
\(\Rightarrow0,4^4< 0,8^3\)

\(4.3^x+3^{x+1}=63\)
\(\Rightarrow4.3^x+3.3^x=63\)
\(\Rightarrow7.3^x=63\Rightarrow3^x=9=3^2\Rightarrow x=2\)
\(9.\left(\dfrac{2}{3}\right)^{x+2}-\left(\dfrac{2}{3}\right)^x=\dfrac{4}{3}\)
\(\Rightarrow9.\left(\dfrac{2}{3}\right)^2\left(\dfrac{2}{3}\right)^x-\left(\dfrac{2}{3}\right)^x=\dfrac{4}{3}\)
\(\Rightarrow9.\dfrac{4}{9}^{ }.\left(\dfrac{2}{3}\right)^x-\left(\dfrac{2}{3}\right)^x=\dfrac{4}{3}\)
\(\Rightarrow\left(\dfrac{2}{3}\right)^x.\left(4-1\right)=\dfrac{4}{3}\)
\(\Rightarrow\left(\dfrac{2}{3}\right)^x.\dfrac{1}{3}=\dfrac{4}{3}\Rightarrow\left(\dfrac{2}{3}\right)^x=4\)
mà \(0< \left(\dfrac{2}{3}\right)^x< 1;4>0;x>0\)
\(\Rightarrow x\in\varnothing\)

Trong 1 phút vòi I chảy được
1
45
bể.
Trong 1 phút vòi II chảy được
1
30
bể.
Trong 1 phút cả hai vòi chảy được
1
45
+
1
30
=
1
18
bể.
Nếu mở cả hai vòi cùng một lúc thì thời gian chảy đầy bể là:
1
:
1
18
=
18
(phút).
Bài giải
Một phút vòi I chảy được:
\(1:45=\dfrac{1}{45}\)(bể)
Một phút vòi II chảy được:
\(1:30=\dfrac{1}{30}\)(bể)
Mở cả hai vòi cùng một lúc thì sau số lâu đầy bể là:
\(1:\left(\dfrac{1}{45}+\dfrac{1}{30}\right)=18\)(phút)
Đ/s: \(18p\)

Ta có:
\(0,3^{30}=0,3^{2.15}=\left(0,3^2\right)^{15}=0,9^{15}\)
\(0,1< 0,9\Rightarrow0,1^{15}< 0,3^{30}\)
so sánh 0,115 và 0,330
0,330 = (0,3)2.15= (0,32)15 = 0,0915 < 0,115
Vậy 0,115 > 0,330
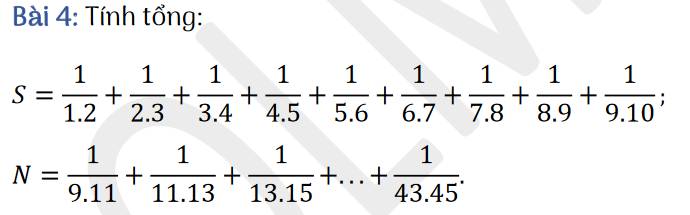
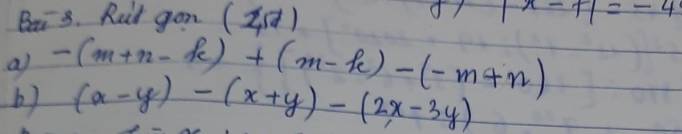
\(A=\left(2x-1\right)^4+3\)
mà \(\left(2x-1\right)^4\ge0,\forall x\)
\(\Rightarrow A=\left(2x-1\right)^4+3\ge0+3=3\)
\(\Rightarrow GTNN\left(A\right)=3\left(x=\dfrac{1}{2}\right)\)
\(B=-\left(8x-\dfrac{4}{5}\right)^6+1\)
mà \(-\left(8x-\dfrac{4}{5}\right)^6\le0,\forall x\)
\(\Rightarrow B=-\left(8x-\dfrac{4}{5}\right)^6+1\le0+1=1\)
\(\Rightarrow GTLN\left(B\right)=1\left(x=\dfrac{1}{10}\right)\)