viết nghiệm và biểu diển tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn:
b) x-y=4Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 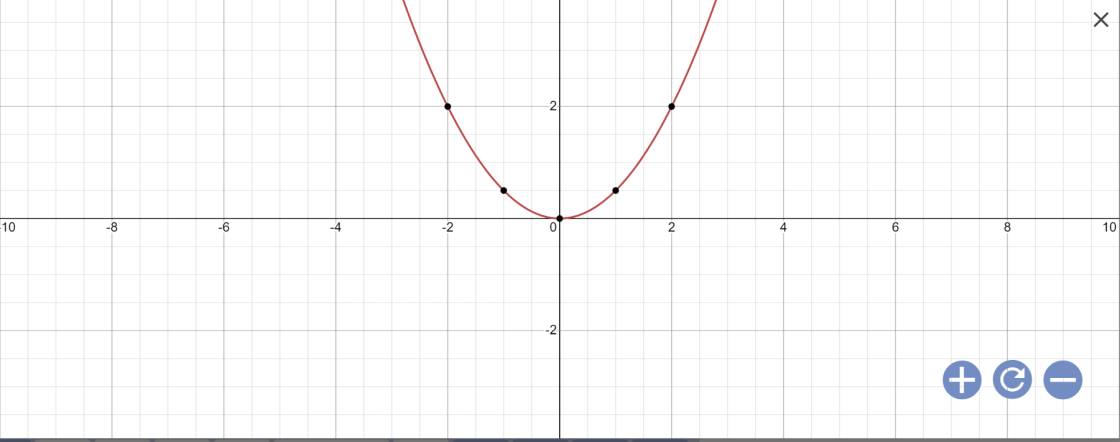
b: Thay x=0 và y=-2 vào (d1), ta được:
\(a\cdot0+b=-2\)
=>b=-2
=>(d1): y=ax-2
Thay x=1 và y=3 vào (d1), ta được:
\(a\cdot1-2=3\)
=>a-2=3
=>a=5
Vậy: (d1): y=5x-2
c: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=2x+m\)
=>\(x^2=4x+2m\)
=>\(x^2-4x-2m=0\)
\(\Delta=\left(-4\right)^2-4\cdot1\cdot\left(-2m\right)=8m+16\)
Để (P) cắt (d2) tại hai điểm phân biệt thì 8m+16>0
=>8m>-16
=>m>-2
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=4\\x_1x_2=\dfrac{c}{a}=-2m\end{matrix}\right.\)
\(x_1+x_2-2x_1x_2=2024\)
=>\(4-2\cdot\left(-2m\right)=2024\)
=>4m+4=2024
=>m+1=506
=>m=505(nhận)

\(x+\sqrt{x+2}=0\left(ĐK:x\ge-2\right)\)
\(\Leftrightarrow x+1+\left(\sqrt{x+2}-1\right)=0\\ \Leftrightarrow x+1+\dfrac{x+2-1}{\sqrt{x+2}+1}=0\\ \Leftrightarrow x+1+\dfrac{x+1}{\sqrt{x+2}+1}=0\\ \Leftrightarrow\left(x+1\right)\left(1+\dfrac{1}{\sqrt{x+2}+1}\right)=0\\ \Rightarrow\left[{}\begin{matrix}x+1=0\\1+\dfrac{1}{\sqrt{x+2}+1}=0\left(PTVN\right)\end{matrix}\right.\Leftrightarrow x=-1\left(TMDK\right)\)
Vậy pt có nghiệm duy nhất: x=-1
Mình giải thích thêm phần này nhé:
\(1+\dfrac{1}{\sqrt{x+2}+1}=0\left(PTVN\right)\)
Vì với mọi x thuộc ĐK:
\(\sqrt{x+2}\ge0\Rightarrow\sqrt{x+2}+1>0\\ \Rightarrow\dfrac{1}{\sqrt{x+2}+1}>0\\ \Rightarrow VT=1+\dfrac{1}{\sqrt{x+2}+1}>0=VP\)
Do VT > VP nên không thể xảy ra dấu =
Dẫn đến ptvn bạn nhé


Với $x>0;x\ne1$:
$P=\frac{\sqrt x+1}{\sqrt x-1}+\frac{2\sqrt x+1}{x-\sqrt x}+\frac{1}{\sqrt x}$
$=\frac{\sqrt x\left(\sqrt x+1\right)}{\sqrt x\left(\sqrt x-1\right)}+\frac{2\sqrt x+1}{\sqrt x\left(\sqrt x-1\right)}+\frac{\sqrt x-1}{\sqrt x\left(\sqrt x-1\right)}$
$=\frac{x+\sqrt x+2\sqrt x+1+\sqrt x-1}{\sqrt x\left(\sqrt x-1\right)}$
$=\frac{x+4\sqrt x}{\sqrt x\left(\sqrt x-1\right)}=\frac{\sqrt x\left(\sqrt x+4\right)}{\sqrt x\left(\sqrt x-1\right)}=\frac{\sqrt x+4}{\sqrt x-1}$
$Toru$

Bài 2:
a: \(\sqrt{\left(2x-1\right)^2}=4\)
=>|2x-1|=4
=>\(\left[{}\begin{matrix}2x-1=4\\2x-1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
b: ĐKXĐ: x>=-1
\(\sqrt{4x+4}-\sqrt{9x+9}-8\sqrt{\dfrac{x+1}{16}}=5\)
=>\(2\sqrt{x+1}-3\sqrt{x+1}-8\cdot\dfrac{\sqrt{x+1}}{4}=5\)
=>\(-3\sqrt{x+1}=5\)
=>\(\sqrt{x+1}=-\dfrac{5}{3}\)(vô lý)
=>Phương trình vô nghiệm
Bài 3:
a: \(Q=\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2}{\sqrt{x}+1}-\dfrac{2}{x-1}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2}{\sqrt{x}+1}-\dfrac{2}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)-2\left(\sqrt{x}-1\right)-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x+\sqrt{x}-2\sqrt{x}+2-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
b: Thay x=9 vào Q, ta được:
\(Q=\dfrac{3}{3+1}=\dfrac{3}{4}\)
Bài 4:
\(\sqrt{x-2\sqrt{x-1}}+\sqrt{x+2\sqrt{x-1}}\)
\(=\sqrt{x-1-2\sqrt{x-1}+1}+\sqrt{x-1+2\sqrt{x-1}+1}\)
\(=\sqrt{\left(\sqrt{x-1}-1\right)^2}+\sqrt{\left(\sqrt{x-1}+1\right)^2}\)
\(=\sqrt{x-1}-1+\sqrt{x-1}+1\left(x>=2\right)\)
\(=2\sqrt{x-1}\)


Em nên viết bằng công thức toán học có biểu tượng Σ góc trái màn hình em nhé. Như vậy mọi người mới hiểu đúng đề được để có thể hỗ trợ tốt nhất cho em.

Ta có:
\(x^2-y^2-4x-25=0\\\Leftrightarrow (x^2-4x+4)-y^2-29=0\\\Leftrightarrow (x-2)^2-y^2=29\\\Leftrightarrow (x-y-2)(x+y-2)=29\)
Vì x, y nguyên nên \(x-y-2;x+y-2\) có giá trị nguyên
\(\Rightarrow x-y-2;x+y-2\) là các ước của 29
Ta có bảng sau:
| x - y - 2 | 1 | 29 | -1 | -29 |
| x + y - 2 | 29 | 1 | -29 | -1 |
| x | 17 | 17 | -13 | -13 |
| y | 14 | -14 | -14 | 14 |
Vì các giá trị tìm được đều thoả mãn x, y nguyên nên \((x;y)=(17;14);(17;-14);(-13;-14);(-13;14)\)
$Toru$





x-y=4
=>y=x-4
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=x-4\end{matrix}\right.\)
Biểu diễn nghiệm: