10^n + 26 chia hết cho 18
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(\dfrac{-5}{19}+\dfrac{7}{23}+\dfrac{-19}{19}\)
\(=\left(\dfrac{-5}{19}+\dfrac{-19}{19}\right)+\dfrac{7}{23}\)
\(=\dfrac{-24}{19}+\dfrac{7}{23}\)
\(=\dfrac{-552}{437}+\dfrac{133}{437}\)
\(=\dfrac{-419}{437}\)
Lời giải:
$\frac{-5}{19}+\frac{7}{23}+\frac{-19}{19}=\frac{7}{23}-\frac{5}{19}-1$
$=\frac{7.19-5.23}{23.19}-1$
$=\frac{18}{437}-1=\frac{-419}{437}$

A = 3 + 22 + 23 + 24 + ... + 22014
2A = 3.2 + 23 + 24 + 25 + ... + 22015
(2A - A) = (22015 + 3.2) - 3
A = 22015 + 6 - 3 = 22015 + 3
Do 22015 = 22015 mà 3 > 1 nên 22015 + 3 > 22015 + 1
⇒ A > B

a) Ta có:
\(-\dfrac{3}{7}>-\dfrac{1}{2}\)
\(\dfrac{4}{-5}< -\dfrac{1}{2}\)
\(\Rightarrow-\dfrac{3}{7}>\dfrac{4}{-5}\)
b) Ta có:
\(\dfrac{-11}{-12}=\dfrac{11}{12}=1-\dfrac{1}{12}\)
\(\dfrac{17}{18}=1-\dfrac{1}{18}\)
Mà: \(\dfrac{1}{18}< \dfrac{1}{12}\)
\(\Rightarrow1-\dfrac{1}{18}>1-\dfrac{1}{12}\)
\(\Rightarrow\dfrac{17}{18}>\dfrac{11}{12}\)
\(\dfrac{-3}{7}\) và \(\dfrac{4}{-5}\)
Ta có : \(\dfrac{-3}{7}\) và \(\dfrac{-4}{5}\)
Mẫu số chung 2 phân số: \(35\).
Ta quy đồng 2 phân số:
\(\dfrac{-3}{7}=\dfrac{-3\cdot5}{7\cdot5}=\dfrac{-15}{35}\)
\(\dfrac{-4}{5}=\dfrac{-4\cdot7}{5\cdot7}=\dfrac{-28}{35}\)
Mà \(\dfrac{15}{35}< \dfrac{28}{35}\) nên \(\dfrac{-15}{35}>\dfrac{-28}{35}\)
Vì vậy \(\dfrac{-3}{7}>\dfrac{4}{-5}\)
\(------------\)
\(\dfrac{-11}{-12}\) và \(\dfrac{17}{18}\)
Ta có:
\(\dfrac{11}{12}\) và \(\dfrac{17}{18}\)
Mẫu số chung 2 phân số: \(36\).
Ta quy đồng 2 phân số:
\(\dfrac{11}{12}=\dfrac{11\times3}{12\times3}=\dfrac{33}{36}\)
\(\dfrac{17}{18}=\dfrac{17\times2}{18\times2}=\dfrac{34}{36}\)
Mà \(\dfrac{33}{36}< \dfrac{34}{36}\) nên \(\dfrac{11}{12}< \dfrac{17}{18}\) hay \(\dfrac{-11}{-12}< \dfrac{17}{18}\)

a) \(-\dfrac{9}{18}+\dfrac{-18}{27}=\dfrac{-1}{2}+\dfrac{-2}{3}=\dfrac{-3}{6}+\dfrac{-4}{6}=\dfrac{-7}{6}\)
b) \(\dfrac{12}{16}-\dfrac{10}{25}=\dfrac{3}{4}-\dfrac{2}{5}=\dfrac{15}{20}-\dfrac{8}{20}=\dfrac{7}{20}\)
c) \(-2+\dfrac{-2}{3}=\dfrac{-6}{3}+\dfrac{-2}{3}=\dfrac{-8}{3}\)
d) \(\dfrac{2}{5}-1=\dfrac{2}{5}-\dfrac{5}{5}=\dfrac{-3}{5}\)
\(#NqHahh\)

câu a)
\(x+\dfrac{2}{4}=\dfrac{3}{6}\\ x=\dfrac{3}{6}-\dfrac{2}{4}\\ x=0\)
câu b)
\(x-\dfrac{1}{6}=\dfrac{1}{-3}\\ x=\dfrac{-1}{3}+\dfrac{1}{6}\\ x=\dfrac{-1}{6}\)

a) \(\dfrac{5}{11}\cdot\dfrac{5}{7}+\dfrac{5}{11}\cdot\dfrac{2}{7}+\dfrac{6}{11}=\dfrac{5}{11}\cdot\left(\dfrac{5}{7}+\dfrac{2}{7}\right)+\dfrac{6}{11}=\dfrac{5}{11}\cdot1+\dfrac{6}{11}=\dfrac{5}{11}+\dfrac{6}{11}=\dfrac{11}{11}=1\)
b) \(\dfrac{3}{13}\cdot\dfrac{6}{11}+\dfrac{3}{13}\cdot\dfrac{9}{11}-\dfrac{3}{13}\cdot\dfrac{4}{11}=\dfrac{3}{13}\cdot\left(\dfrac{6}{11}+\dfrac{9}{11}-\dfrac{4}{11}\right)=\dfrac{3}{13}\cdot\dfrac{11}{11}=\dfrac{3}{13}\cdot1=\dfrac{3}{13}\)
c) \(\dfrac{-5}{6}\cdot\dfrac{4}{19}+\dfrac{7}{12}\cdot\dfrac{4}{-19}-\dfrac{40}{57}=\dfrac{-5}{6}\cdot\dfrac{4}{19}+\dfrac{-7}{12}\cdot\dfrac{4}{19}-\dfrac{40}{57}=\dfrac{4}{19}\cdot\left(\dfrac{-5}{6}+\dfrac{-7}{12}\right)-\dfrac{40}{57}\)
\(=\dfrac{4}{19}\cdot\dfrac{-17}{12}-\dfrac{40}{47}=\dfrac{-17}{57}-\dfrac{40}{57}=\dfrac{-57}{57}=-1\)
d) \(\left(\dfrac{11}{4}\cdot\dfrac{-5}{9}+\dfrac{4}{9}\cdot\dfrac{11}{-4}\right)\cdot\dfrac{8}{33}=\left(\dfrac{11}{4}\cdot\dfrac{-5}{9}+\dfrac{-4}{9}\cdot\dfrac{11}{4}\right)\cdot\dfrac{8}{33}=\dfrac{11}{4}\cdot\dfrac{8}{33}\cdot\left(\dfrac{-5}{9}+\dfrac{-4}{9}\right)\)
\(=\dfrac{11}{4}\cdot\dfrac{8}{33}\cdot1=\dfrac{11\cdot8}{4\cdot33}=\dfrac{2}{3}\)
e) \(\left(\dfrac{12}{61}-\dfrac{31}{22}+\dfrac{14}{91}\right)\cdot\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)=\left(\dfrac{12}{61}-\dfrac{31}{22}+\dfrac{14}{91}\right)\cdot\left(\dfrac{1}{6}-\dfrac{1}{6}\right)\)
\(=\left(\dfrac{12}{61}-\dfrac{31}{22}+\dfrac{14}{91}\right)\cdot0=0\)
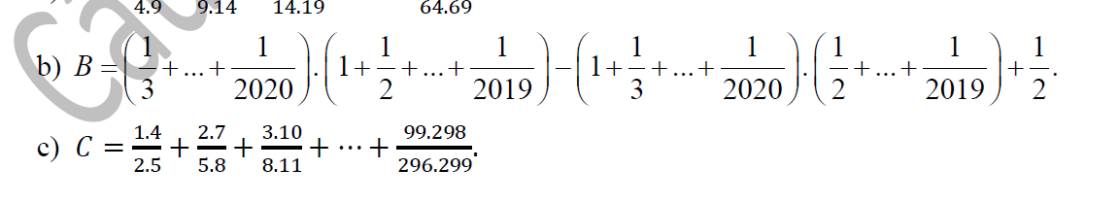
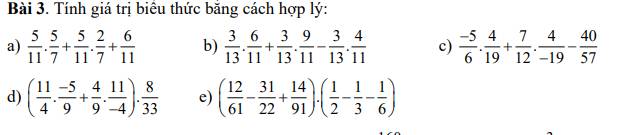
Cần bổ sung thêm điều kiện $n$ là số tự nhiên lớn hơn $0$.
CMR: $10^n+26\vdots 18$
(lần sau bạn lưu ý đăng đề cho đầy đủ nhé)
Lời giải:
Với $n\in\mathbb{N}^*$, $10^n+26$ là số chẵn
$\Rightarrow 10^n+26\vdots 2(1)$
Mặt khác:
$10\equiv 1\pmod 9$
$\Rightarrow 10^n\equiv 1^n\equiv 1\pmod 9$
$\Rightarrow 10^n+26\equiv 1+26=27\equiv 0\pmod 9$
$\Rightarrow 10^n+26\vdots 9(2)$
Từ $(1); (2)$, mà $(2,9)=1$ nên $10^n+26\vdots (2.9)$ hay $10^n+26\vdots 18$.