a^2.b/2a^2+b^3+2/3>=a^2+ab/2a^2+b^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=1997.1999=\left(1998-1\right)\left(1998+1\right)=1998^2-1< 1998^2=B\)

I'll let you do the drawing.
a) Consider the 2 triangles AHM and ABH, which both have a common angle at A, have \(\widehat{AMH}=\widehat{AHB}\left(=90^o\right)\). Therefore, \(\Delta AHM~\Delta ABH\left(a.a\right)\). This means \(\dfrac{AH}{AB}=\dfrac{AM}{AH}\) or \(AH^2=AM.AB\)
Similarly, we have \(AH^2=AN.AC\). From these, we get \(AM.AB=AN.AC=AH^2\)
We can easily prove that AMHN is a rectangle (because \(\widehat{MAN}=\widehat{AMH}=\widehat{ANH}=90^o\)). Thus, \(AH=MN\)(2 diagonals of a rectangle are equal)
And finally, we get \(AM.AB=AN.AC=MN^2\), and that's what we must prove!
b) We can easily prove \(HN//AB\left(\perp AC\right)\), which means \(\widehat{FHN}=\widehat{B}\)
Consider the right triangle BHM (right at M), it has the median ME. Therefore, \(ME=\dfrac{BH}{2}\). We also have \(BE=\dfrac{BH}{2}\) so \(ME=BE\) or \(\Delta BEM\) is an isosceles triangle, or \(\widehat{BEM}=180^o-2.\widehat{B}\)
Similarly, we have \(\widehat{HFN}=180^o-2.\widehat{FHN}\)
We have already had \(\widehat{B}=\widehat{FHN}\). Thus, \(\widehat{BEM}=\widehat{HFN}\) or \(ME//NF\) (2 equal staggered angles)
Therefore, MEFN is a trapezoid.
In this trapezoid, I is the midmpoint of EF, O is the midpoint of MN (2 diagonal AH, MN of the rectangle AMHN meets at O). Thus, OI is the avergage line of the trapezoid MEFN (ME//NF) or \(OI//NF\)
It's easy to see \(\widehat{FNC}=\widehat{C}\); \(\widehat{MNH}=\widehat{MAH}\)
Also, \(\widehat{C}=\widehat{MAH}\left(=90^o-\widehat{B}\right)\). So, \(\widehat{FNC}=\widehat{MNH}\) or \(\widehat{FNC}+\widehat{FNH}=\widehat{MNH}+\widehat{FNH}\) or \(\widehat{CNH}=\widehat{MNF}\). Because \(\widehat{CNH}=90^o\), it's easy to see \(\widehat{MNF}=90^o\) or \(NF\perp MN\)
We have already prove that \(OI//NF\). Therefore, \(OI\perp MN\), and that's what we must prove!
c) I'm thinking about this question.

cái này đáng ra là tìm giá trị lớn nhất chứ không phải nhỏ nhất
p = 2 + x - x2
P = -x2 + x + 2
P = - ( x2 - 2. \(\dfrac{1}{2}\)x + \(\dfrac{1}{4}\)) + \(\dfrac{9}{4}\)
P = - (x - \(\dfrac{1}{2}\))2 + \(\dfrac{9}{4}\)
- ( x - 1/2 ) 2 ≤ 0 ⇔ p ≤ \(\dfrac{9}{4}\)⇔ P(max) = 9/4 dấu = xảy ra khi x = 1/2

\(a^3-x-x^3+a=0\)
\(\Leftrightarrow a^3-x^3+\left(a-x\right)=0\)
\(\Leftrightarrow\left(a-x\right)\left(a^2+ax+x^2\right)+\left(a-x\right)=0\)
\(\Leftrightarrow\left(a-x\right)\left(a^2+ax+x^2+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=x\\a^2+ax+x^2+1=0\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\Leftrightarrow a^2+ax+x^2+1=0\)
Ta có:\(a^2+ax+x^2+1=a^2+2.a.\dfrac{1}{2}x+\dfrac{1}{4}x^2+\dfrac{3}{4}y^2+1\)
\(=\left(a+\dfrac{1}{2}x\right)^2+\dfrac{3}{4}y^2+1>0\)
\(\Rightarrow\left(2\right)\) vô lý
Vậy \(a=x\)

\(B=x^{2020}-2018x^{2019}-2018x^{2018}-...-2018x+1\)
\(=x^{2020}-2019x^{2019}+x^{2019}-2019x^{2018}+x^{2018}-2019x^{2017}+...+x^2-2019x+x+1\)
\(=x^{2019}\left(x-2019\right)+x^{2018}\left(x-2019\right)+x^{2017}\left(x-2019\right)+...+x\left(x-2019\right)+x+1\)Thay \(x=2019\) vào B ta có:
\(B=2019^{2019}\left(2019-2019\right)+2019^{2018}\left(2019-2019\right)+2019^{2017}\left(2019-2019\right)+...+2019\left(2019-2019\right)+2019+1\)
\(=2019+1=2020\)

.2,đk x >= 0 ; x khác 1
\(P=\left(\dfrac{2x+1-\sqrt{x}\left(\sqrt{x}-1\right)}{x\sqrt{x}-1}\right)\left(\dfrac{1+x\sqrt{x}-\sqrt{x}-x}{\sqrt{x}+1}\right)\)
\(=\dfrac{x+\sqrt{x}+1}{x\sqrt{x}-1}\left(\dfrac{x\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)}{\sqrt{x}+1}\right)\)
\(=\dfrac{\left(x-1\right)\left(\sqrt{x}-1\right)}{\left(x-1\right)}=\sqrt{x}-1\)
Ta có \(\sqrt{x}-1=3\Leftrightarrow x=16\left(tm\right)\)

phương pháp
giả sử tồn tại n để \(\dfrac{n+20}{n+90}\) là bình phương của một số hữu tỉ thì sẽ tồn tại một phân số \(\dfrac{a}{b}\) thỏa mãn
\(\dfrac{n+20}{n+90}\) = ( \(\dfrac{a}{b}\))2
⇔ b2 - a2 = 70 ⇔ (b-a)(b+a) = 70 = 10 . 7 = 14 x 5 = 35 x 2
với a,b là các số tự nhiên thì \(\left\{{}\begin{matrix}b-a=7\\a+b=10\end{matrix}\right.\) vô nghiệm tương tự
các trường hợp còn lại cũng vô nghiệm vậy ko có giá trị nào của n thỏa mãn đề bài
đây là phương pháp phản chứng nhé bạn
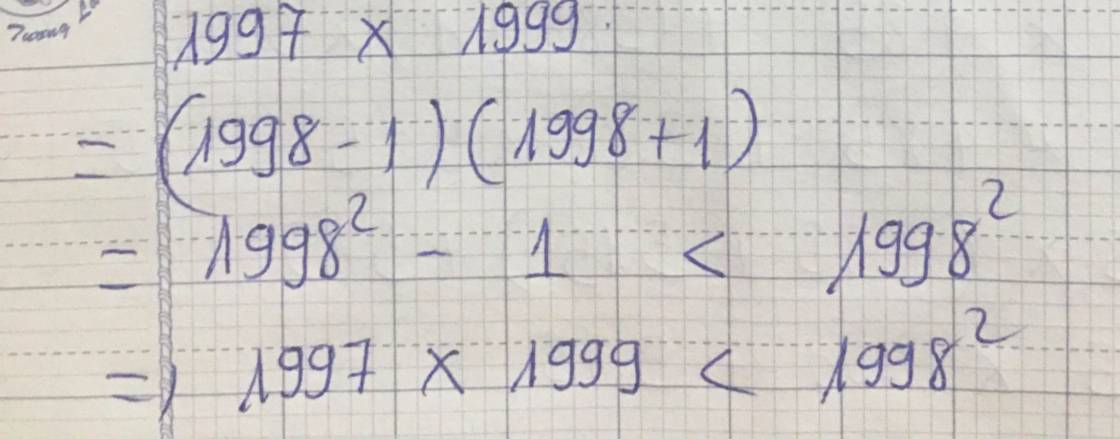
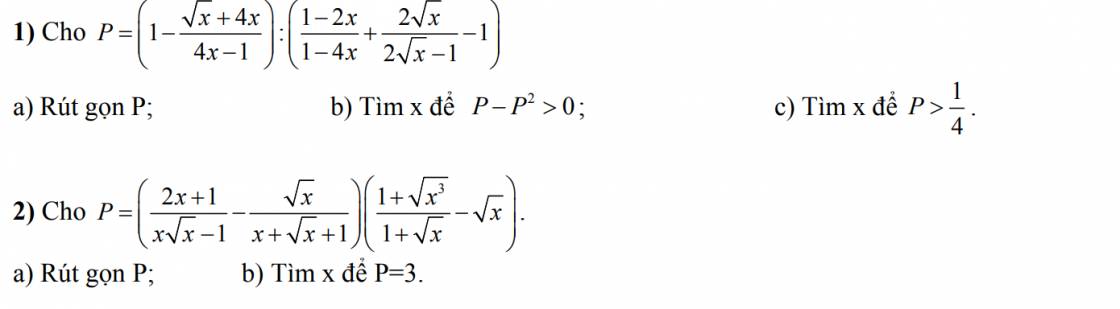
Em nên gõ công thức trực quan để được hỗ trợ tốt hơn nhé
Bạn chịu khó đánh chữ bằng Latex ra nhé.