Điều kiện: \(x\ne0\)

\(\dfrac{x}{2}-\dfrac{1}{x}=\dfrac{1}{12}\\ \Leftrightarrow6x^2-12-x=0\\ \Leftrightarrow6x^2-9x+8x-12=0\\ \Leftrightarrow3x\left(2x-3\right)+4\left(2x-3\right)=0\\ \Leftrightarrow\left(3x+4\right)\left(2x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{4}{3}\\x=\dfrac{3}{2}\end{matrix}\right.\left(tm\right)}\)

tính giúp mình với

\(C=\left|-3\left(\dfrac{-13}{15}-\dfrac{17}{21}\right)\right|-\left|\dfrac{-13}{15}+\dfrac{17}{7}\right|+\left(-12+\dfrac{35}{3}\right):\left|-\dfrac{7}{6}\right|\\ =\left|-3.-\dfrac{176}{105}\right|-\left|-\dfrac{6}{35}\right|+\left(-\dfrac{1}{3}\right):\dfrac{7}{6}\\ =\dfrac{176}{35}-\dfrac{6}{35}-\dfrac{1}{3}:\dfrac{7}{6}\\ =\dfrac{176}{35}-\dfrac{6}{35}-\dfrac{2}{7}\\ =\dfrac{170}{35}-\dfrac{2}{7}=\dfrac{32}{7}.\)

tính giúp mình với mình đang cần gấp

\(\left(\dfrac{1}{27}\right)^5\) = \(\left(\dfrac{1}{3^3}\right)^5\) = \(\left(\dfrac{1}{3}\right)^{15}\)

\(\left(\dfrac{1}{27}\right)^5=\left[\left(\dfrac{1}{3}\right)^3\right]^5=\dfrac{1}{3}^{3.5}=\dfrac{1}{3}^{15}\)

bn hểu ko

`#040911`

a)

Ta có:

\(\left\{{}\begin{matrix}\text{AB = AC (tg ABC cân tại A)}\\\text{BD = CE (gt)}\end{matrix}\right.\)

`\Rightarrow \text {AD = AE}`

Xét `\Delta ADE:`

`AD = AE`

`\Rightarrow Delta ADE` cân tại A

`\Rightarrow`\(\widehat{\text{ADE}}=\widehat{\text{AED}}=\dfrac{180^0-\widehat{\text{A}}}{2}\) `(1)`

`\Delta ABC` cân tại A

`\Rightarrow`\(\widehat{\text{ABC}}=\widehat{\text{ACB}}=\dfrac{180^0-\widehat{\text{A}}}{2}\) `(2)`

Từ `(1)` và `(2)`

`\Rightarrow`\(\widehat{\text{ABC}}=\widehat{\text{ADE}}\)

Mà `2` góc này nằm ở vị trí đồng vị

`\Rightarrow \text {DE // BC (t/c 2 dt' //)}`

b)

Ta có:

\(\widehat{ABC}=\widehat{ACB}\text{ }\left(\Delta ABC\text{ cân tại A}\right)\)

Mà \(\left\{{}\begin{matrix}\widehat{ABC}=\widehat{MBD}\text{ }\left(\text{đối đỉnh}\right)\\\widehat{ACB}=\widehat{NCE}\text{ }\left(\text{đối đỉnh}\right)\end{matrix}\right.\) 

`\Rightarrow`\(\widehat{\text{MBD}}=\widehat{\text{NCE}}\)

Xét `\Delta MBD` và `\Delta NCE:`

\(\widehat{\text{BMD}}=\widehat{\text{CNE}}\left(=90^0\right)\)

\(\text{BD = CE (gt)}\)

\(\widehat{\text{MBD}}=\widehat{\text{NCE}}\text{ (CMT)}\)

`\Rightarrow Delta MBD = \Delta NCE (ch - gn)`

`\Rightarrow \text {DM = EN (2 cạnh tương ứng)}`

c)

Vì `\Delta MBD = \Delta NCE (b)`

`\Rightarrow \text {BM = CN (2 cạnh tương ứng)}`

Ta có:

\(\left\{{}\begin{matrix}\widehat{\text{ABM}}+\widehat{\text{ABC}}=180^0\text{ (kề bù)}\\\widehat{\text{ACN}}+\widehat{\text{ACB}}=180^0\text{ (kề bù)}\end{matrix}\right.\)

Mà \(\widehat{\text{ABC}}=\widehat{\text{ACB}}\) `(\Delta ABC` cân tại A`)`

`\Rightarrow`\(\widehat{\text{ABM}}=\widehat{\text{ACN}}\)

Xét `\Delta AMB` và `\Delta ANC:`

\( \text{AB = AC }\left(\Delta\text{ABC cân tại A}\right)\\ \widehat{\text{ABM}}=\widehat{\text{ACN}}\\ \text{BM = CN (CMT)}\)

`\Rightarrow \Delta AMB = \Delta ANC (c-g-c)`

`\Rightarrow \text {AM = AN (2 cạnh tương ứng)}`

Xét `\Delta AMN`

`\text {AM = AN}`

`\Rightarrow \Delta AMN` là `\Delta` cân.

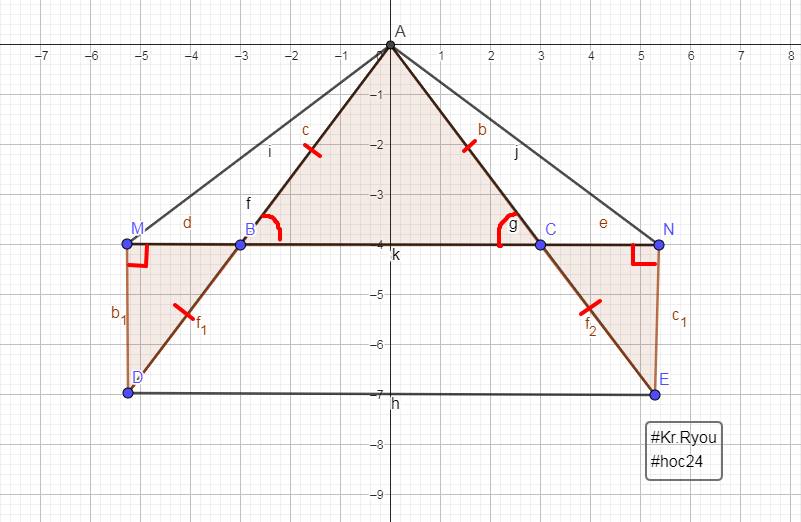
bn ơi mình thấy câu b kẻ thêm nó cứ sao ý

bn có chép đúng đề bài ko