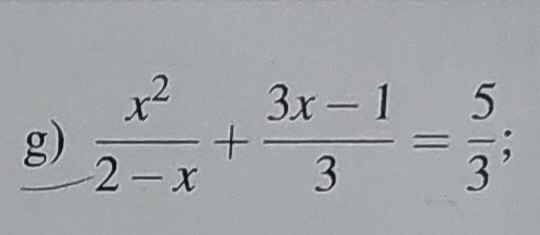
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 2x-3y=5
=>2x=3y+5
=>\(x=\dfrac{3}{2}y+\dfrac{5}{2}\)
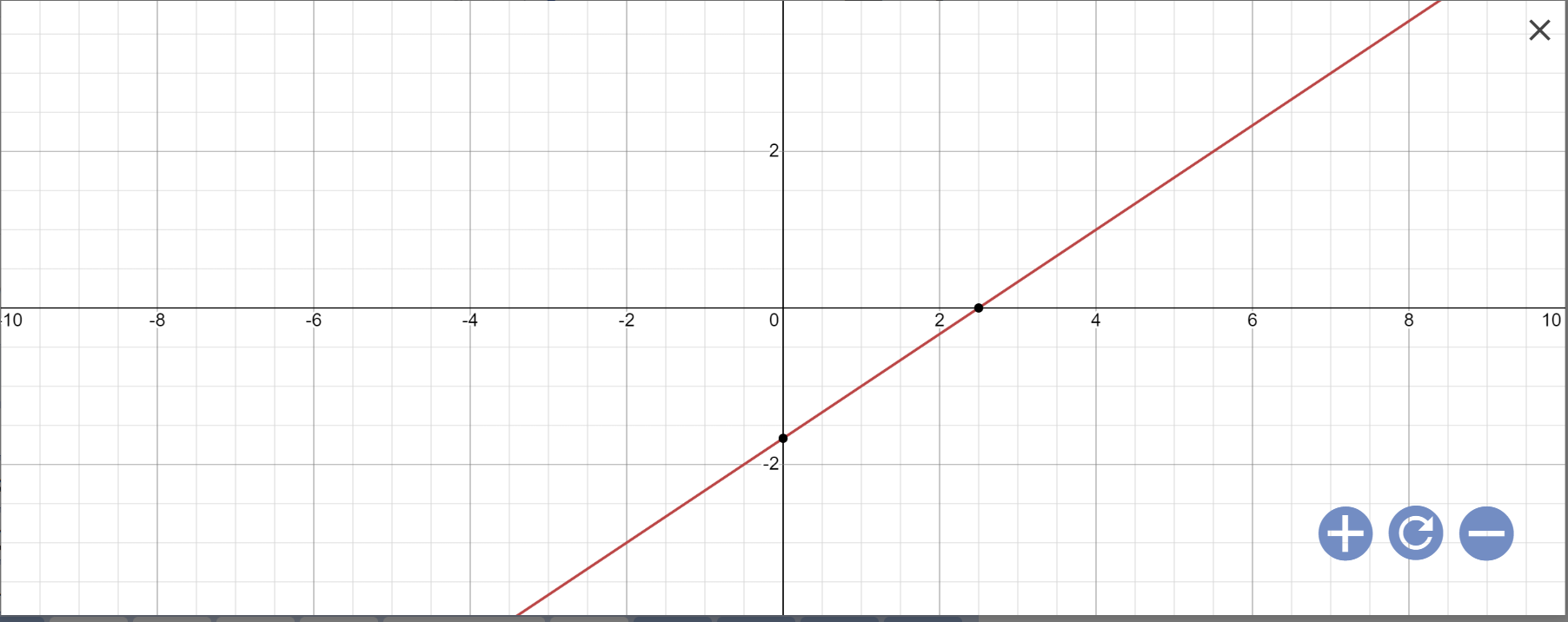
vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}y\in R\\x=\dfrac{3}{2}y+\dfrac{5}{2}\end{matrix}\right.\)
Biểu diễn:
b: 0x+y=3
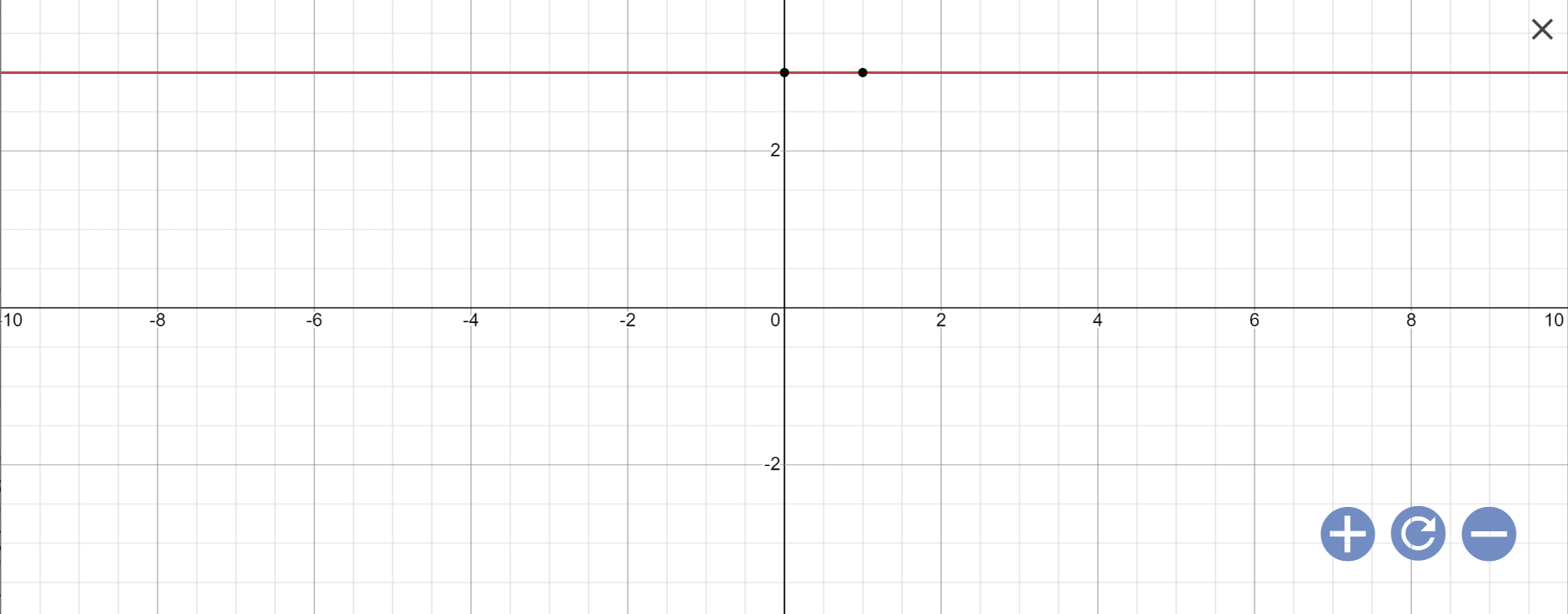
=>y=3
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=3\end{matrix}\right.\)
Biểu diễn:
c: x+0y=-2
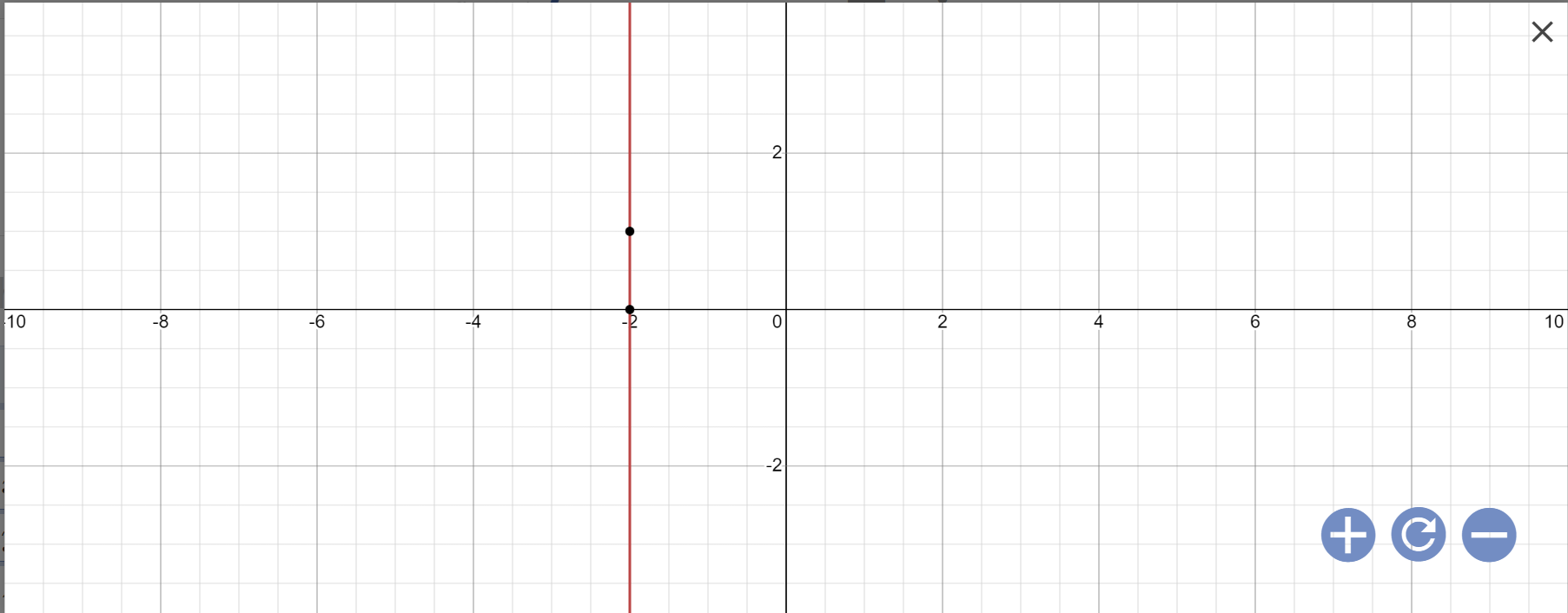
=>x=-2
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x=-2\\y\in R\end{matrix}\right.\)
Biểu diễn:

ĐKXĐ: \(x\ne-5\)
\(\dfrac{x+6}{x+5}+\dfrac{3}{2}=2\)
\(\Leftrightarrow\dfrac{x+6}{x+5}=\dfrac{1}{2}\)
\(\Rightarrow2\left(x+6\right)=1.\left(x+5\right)\)
\(\Leftrightarrow2x+12=x+5\)
\(\Leftrightarrow2x-x=5-12\)
\(\Leftrightarrow x=-7\) (tm ĐKXĐ)
ĐKXĐ: \(x\ne-5\)
\(\dfrac{x+6}{x+5}+\dfrac{3}{2}=2\)
=>\(\dfrac{x+6}{x+5}=2-\dfrac{3}{2}=\dfrac{1}{2}\)
=>\(2\left(x+6\right)=x+5\)
=>\(2x+12=x+5\)
=>2x-x=5-12
=>x=-7(nhận)

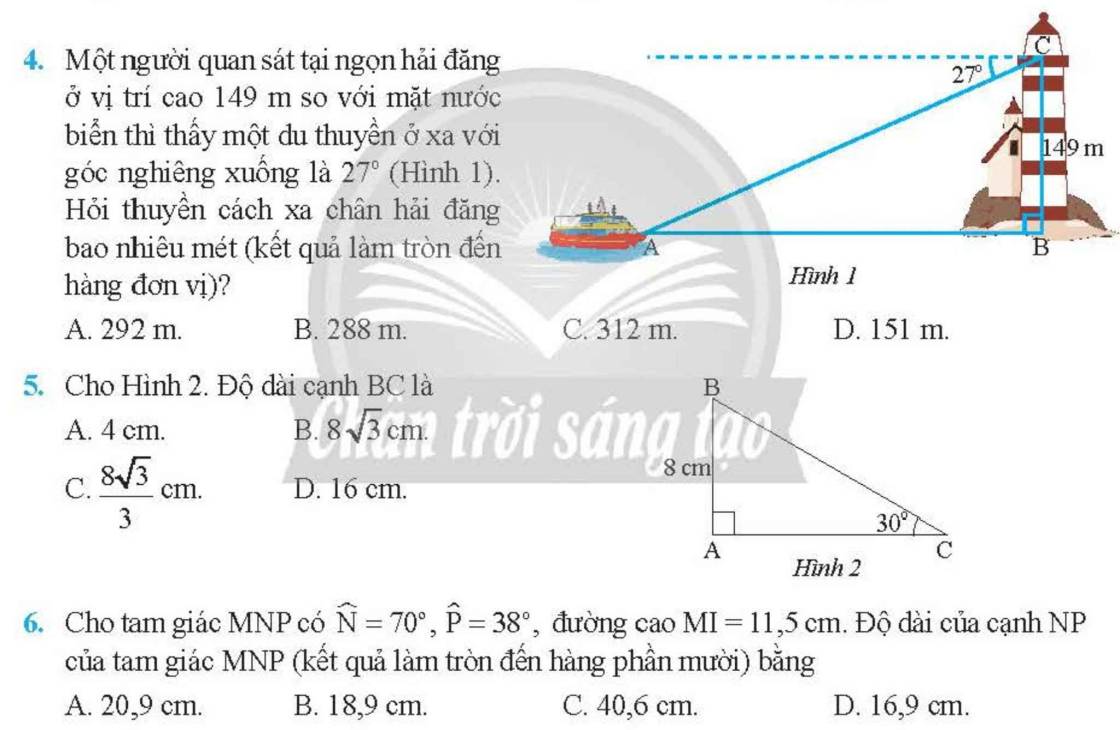
6:
Xét ΔMIN vuông tại I có \(tanN=\dfrac{MI}{NI}\)
=>\(NI=\dfrac{MI}{tanN}=\dfrac{11.5}{tan70}\simeq4,2\left(cm\right)\)
Xét ΔMIP vuông tại I có \(tanP=\dfrac{MI}{IP}\)
=>\(IP=\dfrac{MI}{tanP}=\dfrac{11.5}{tan38}\simeq14,7\left(cm\right)\)
NP=NI+IP=4,2+14,7=18,9(cm)
=>Chọn B
5: Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}\)
=>\(BC=\dfrac{8}{sin30}=16\left(cm\right)\)
=>Chọn D
4:
\(\widehat{BAC}=27^0\)
Xét ΔBAC vuông tại B có \(tanBAC=\dfrac{BC}{BA}\)
=>\(BA=\dfrac{149}{tan27}\simeq292\left(m\right)\)
=>Chọn A

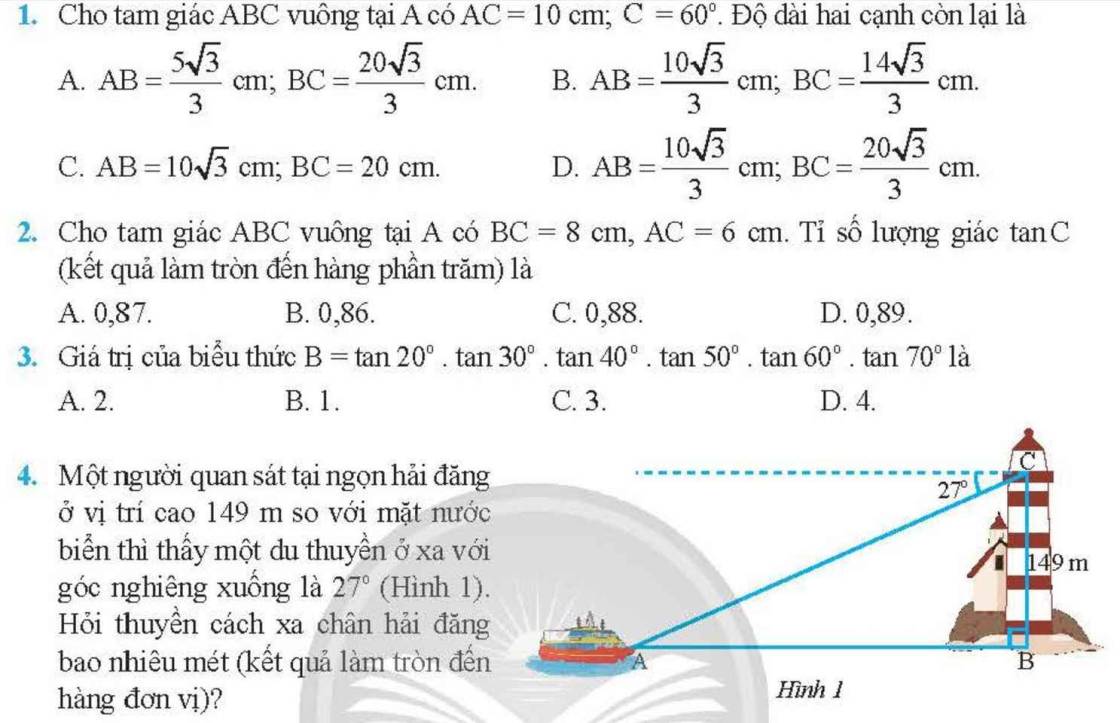
1: Xét ΔABC vuông tại A có \(tanC=\dfrac{AB}{AC}\)
=>\(\dfrac{AB}{10}=tan60\)
=>\(AB=10\cdot tan60=10\sqrt{3}\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\)
=>Chọn C
2: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(AB=\sqrt{8^2-6^2}=\sqrt{28}=2\sqrt{7}\left(cm\right)\)
Xét ΔABC vuông tại A có \(tanC=\dfrac{AB}{AC}=\dfrac{2\sqrt{7}}{6}=\dfrac{\sqrt{7}}{3}\cong0,88\)
=>Chọn C
3: \(B=tan20\cdot tan30\cdot tan40\cdot tan50\cdot tan60\cdot tan70\)
\(=\left(tan20\cdot tan70\right)\cdot\left(tan30\cdot tan60\right)\cdot\left(tan40\cdot tan50\right)\)
=1*1*1
=1
=>Chọn B
4:
\(\widehat{BAC}=27^0\)
Xét ΔBAC vuông tại B có \(tanBAC=\dfrac{BC}{BA}\)
=>\(BA=\dfrac{149}{tan27}\simeq292\left(m\right)\)
Vậy: Thuyền cách xa chân hải đăng 292m

Ta có:
\(4A+3B-\left(4A+2B\right)=x^2-2x+1-\left(x^2-2x+9\right)\)
\(\Rightarrow B=-8\)
Thay B vào \(4A+2B=x^2-2x+9\) được:
\(4A+2.\left(-8\right)=x^2-2x+9\)
\(\Rightarrow4A=x^2-2x+9+16\)
\(\Rightarrow4A=x^2-2x+25\)
\(\Rightarrow A=\dfrac{x^2-2x+25}{4}\)
Vậy...
\(\left\{{}\begin{matrix}4A+2B=x^2-2x+9\\4A+3B=x^2-2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\4A+3B=x^2-2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\4A+3.\left(-8\right)=x^2-2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\4A-24=x^2-2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\4A=x^2-2x+25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\A=\dfrac{x^2-2x+25}{4}\end{matrix}\right.\)

\(B=\dfrac{A.\left(x+16\right)}{5}\left(x\ge0\right)\\ =\dfrac{5}{3+\sqrt{x}}.\dfrac{x+16}{5}=\dfrac{x+16}{\sqrt{x}+3}\\ =\dfrac{x-9}{\sqrt{x}+3}+\dfrac{25}{\sqrt{x}+3}\\ =\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\sqrt{x}+3}+\dfrac{25}{\sqrt{x}+3}\\ =\sqrt{x}-3+\dfrac{25}{\sqrt{x}+3}\\ =\left(\sqrt{x}+3+\dfrac{25}{\sqrt{x}+3}\right)-6\)
\(\ge2\sqrt{\left(\sqrt{x}+3\right).\dfrac{25}{\sqrt{x}+3}}-6=2\sqrt{25}-6=4\) (Áp dụng BĐT Cô Si. Do \(\sqrt{x}+3,\dfrac{25}{\sqrt{x}+3}>0\forall x\inĐK\))
Dấu = xảy ra khi: \(\sqrt{x}+3=\dfrac{25}{\sqrt{x}+3}\Leftrightarrow\left(\sqrt{x}+3\right)^2=25\Rightarrow\sqrt{x}+3=5\)
\(\Leftrightarrow x=4\left(TMDK\right)\)
Vậy GTNN B là: 4 tại x=4

Vậy giá trị của PPP là 222 trong trường hợp có nghiệm a=1a = 1a=1, b=1b = 1b=1, c=0c = 0c=0.
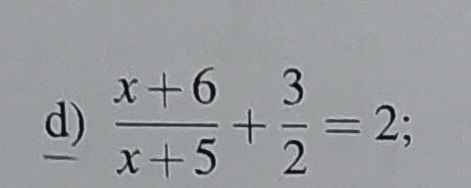
ĐKXĐ: \(x\ne2\)
\(\dfrac{x^2}{2-x}+\dfrac{3x-1}{3}=\dfrac{5}{3}\)
\(\Leftrightarrow\dfrac{x^2}{2-x}=\dfrac{5}{3}-\dfrac{3x-1}{3}\)
\(\Leftrightarrow\dfrac{x^2}{2-x}=\dfrac{6-3x}{3}\)
\(\Leftrightarrow\dfrac{x^2}{2-x}=2-x\)
\(\Rightarrow x^2=\left(2-x\right)^2\)
\(\Leftrightarrow x^2=x^2-4x+4\)
\(\Leftrightarrow4x=4\)
\(\Leftrightarrow x=1\) (tm ĐKXĐ)