chứng minh một tam giác trong gương bằng một tam giác
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
QL
3
NV
Nguyễn Việt Dũng
CTVVIP
9 tháng 3
- "Đánh kẻ chạy đi": Ý nói ta nên trừng trị những kẻ cố tình làm sai, trốn tránh trách nhiệm.
- "Không đánh người chạy lại": Ý nói ta nên có lòng nhân ái, vị tha với những người đã biết nhận ra sai lầm và cố gắng sửa chữa.
8 tháng 3
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{BAD}\) chung
AD=AE
Do đó: ΔABD=ΔACE
b: Ta có: ΔABD=ΔACE
=>\(\widehat{ABD}=\widehat{ACE}\)
Ta có: \(\widehat{ABD}+\widehat{CBD}=\widehat{ABC}\)
\(\widehat{ACE}+\widehat{ECB}=\widehat{ACB}\)
mà \(\widehat{ABD}=\widehat{ACE}\) và \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{CBD}=\widehat{ECB}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
c: ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: IB=IC
=>I nằm trên đường trung trực của BC(2)
ta có: MB=MC
=>M nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,I,M thẳng hàng
8 tháng 3
a: Ta có: ΔCAB cân tại C
=>\(\widehat{CAB}=\widehat{CBA}\)
mà \(\widehat{CBA}=50^0\)
nên \(\widehat{CAB}=50^0\)
Ta có: ΔCAB cân tại C
=>\(\widehat{ACB}=180^0-2\cdot\widehat{CAB}=80^0\)
Xét ΔCAB có \(\widehat{ACB}>\widehat{CAB}=\widehat{CBA}\)
mà AB,CB,CA lần lượt là cạnh đối diện của các góc ACB,CAB,CBA
nên AB>CB=CA
b: Xét ΔCIA vuông tại I và ΔCIB vuông tại I có
CA=CB
CI chung
Do đó: ΔCIA=ΔCIB
=>IA=IB
c: Ta có: ΔCIA=ΔCIB
=>\(\widehat{ACI}=\widehat{BCI}\)
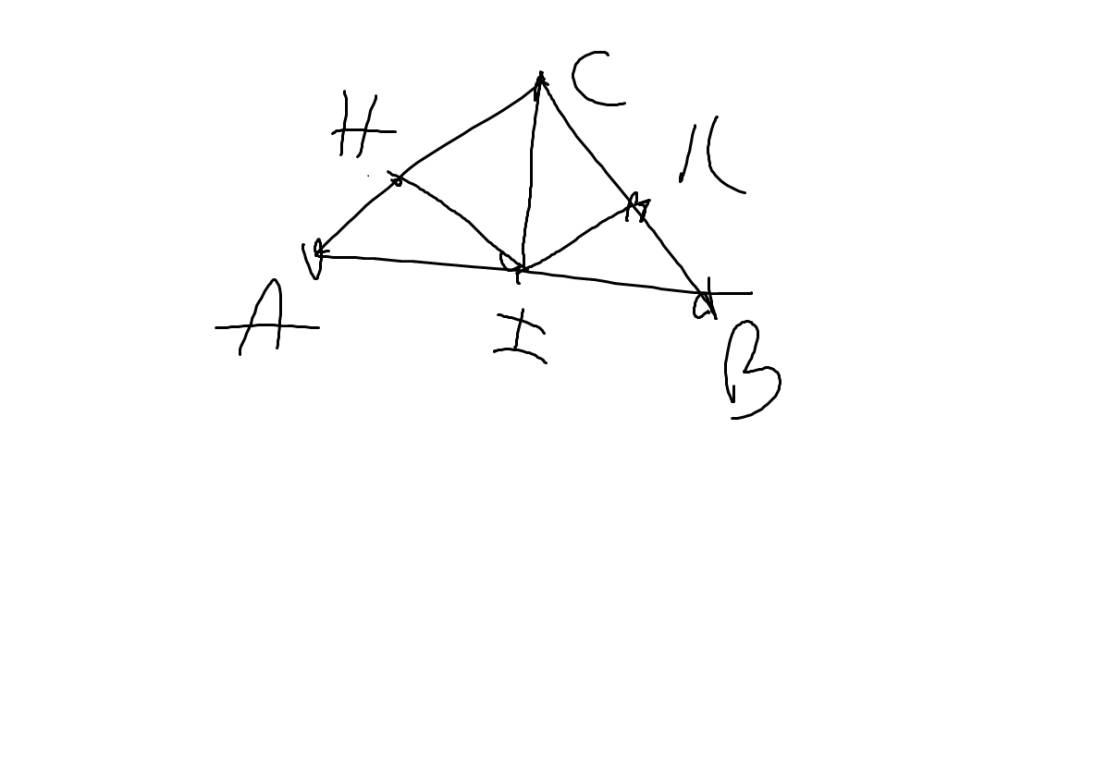
Xét ΔCHI vuông tại H và ΔCKI vuông tại K có
CI chung
\(\widehat{HCI}=\widehat{KCI}\)
Do đó: ΔCHI=ΔCKI
=>IH=IK
d: Ta có: ΔCHI=ΔCKI
=>CH=CK
=>ΔCHK cân tại C
8 tháng 3
Bài 2:
a: Xét ΔOAD và ΔOCB có
OA=OB
\(\widehat{AOD}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
b: Ta có: ΔOAD=ΔOCB
=>\(\widehat{ODA}=\widehat{OBC};\widehat{OAD}=\widehat{OCB}\)
Ta có: \(\widehat{OAD}+\widehat{DAB}=180^0\)(hai góc kề bù)
\(\widehat{OCB}+\widehat{DCB}=180^0\)(hai góc kề bù)
mà \(\widehat{OAD}=\widehat{OCB}\)
nên \(\widehat{DAB}=\widehat{DCB}\)
Ta có: OA+AB=OB
OC+CD=OD
mà OA=OC và OB=OD
nên AB=CD
Xét ΔIAB và ΔICD có
\(\widehat{IAB}=\widehat{ICD}\)
AB=CD
\(\widehat{IBA}=\widehat{IDC}\)
Do đó: ΔIAB=ΔICD
c: Sửa đề: OI là phân giác của góc xOy
Ta có: ΔIAB=ΔICD
=>IB=ID và IA=IC
Xét ΔOIB và ΔOID có
OB=OD
IB=ID
OI chung
Do đó: ΔOIB=ΔOID
=>\(\widehat{BOI}=\widehat{DOI}\)
=>\(\widehat{xOI}=\widehat{yOI}\)
=>OI là phân giác của góc xOy
d: Sửa đề: OI\(\perp\)BD
ta có: OB=OD
=>O nằm trên đường trung trực của BD(1)
ta có: IB=ID
=>I nằm trên đường trung trực của BD(2)
Từ (1),(2) suy ra OI là đường trung trực của BD
=>OI\(\perp\)BD
e: Xét ΔOBD có \(\dfrac{OA}{AB}=\dfrac{OC}{CD}\)
nên AC//BD
Bài 1:
a: ΔABC vuông cân tại A
=>AB=AC và \(\widehat{ABC}=\widehat{ACB}=45^0\)
Ta có: BO là phân giác của góc ABC
=>\(\widehat{ABO}=\widehat{CBO}=\dfrac{\widehat{ABC}}{2}=22,5^0\)
ta có: CO là phân giác của góc ACB
=>\(\widehat{ACO}=\widehat{BCO}=\dfrac{\widehat{ACB}}{2}=22,5^0\)
b: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\left(=22,5^0\right)\)
nên ΔOBC cân tại O
c: Ta có: ΔOBC cân tại O
=>\(\widehat{BOC}=180^0-2\cdot\widehat{OBC}=180^0-2\cdot22,5^0=135^0\)
d: Xét ΔAMC vuông tại A và ΔANB vuông tại A có
AC=AB
\(\widehat{ACM}=\widehat{ABN}\left(=22,5^0\right)\)
Do đó: ΔAMC=ΔANB
=>MC=BN
Ta có: OM+OC=CM
ON+OB=BN
mà OC=OB và CM=BN
nên OM=ON
Ta có: ΔAMC=ΔANB
=>AM=AN
Xét ΔAMO và ΔANO có
AM=AN
MO=NO
AO chung
Do đó: ΔAMO=ΔANO
=>\(\widehat{AOM}=\widehat{AON}\)
=>OA là phân giác của góc MON
e: Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC
f: ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)CB
NM
2
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3
\(6x=3y=5z\Rightarrow\dfrac{x}{5}=\dfrac{y}{10}=\dfrac{z}{6}\)
Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{x}{5}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{2x}{10}=\dfrac{3y}{30}=\dfrac{z}{6}=\dfrac{2x+3y+z}{10+30+6}=\dfrac{-92}{46}=-2\)
\(\Rightarrow\left\{{}\begin{matrix}x=-2.5=-10\\y=-2.10=-20\\z=-2.6=-12\end{matrix}\right.\)
8 tháng 3
6x=5y
=>\(\dfrac{x}{5}=\dfrac{y}{6}\)
mà 2x-y=44
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{2x-y}{2\cdot5-6}=\dfrac{44}{4}=11\)
=>\(x=11\cdot5=55;y=11\cdot6=66\)