Khi chuyển dấu phẩy của một số thập phân sang bên phải 1 hàng thì ta được số mới bằng 10 lần số cũ

Do đó, tổng của số mới và số phải tìm bằng:

\(10+1=11\) (lần số phải tìm)

Số phải tìm là:

\(28,908:11=2,628\)

Đáp số: 2,628

Khi chuyển dấu phẩy sang phải một hàng thì ta được số mới bằng 10 lần số cũ

11 lần số cũ là 10 số cũ+số cũ=số mới+số cũ=28,908

Số cũ là 28,908:11=2,628

 2) Mình làm rồi nhé !

1) 

\(a.3,265\times100=326,5\\ b.5,4\times1000=540\\ c.0,386\times10=3,86\\ d.0,02\times1000=20\\ e.75,2:10=7,52\\ f.8127:100=81,27\\ g.5,24:100=0,0524\\ h.74,8:1000=0,0748\\ i.52:100=0,52\\ k.0,7:1000=0,0007\\ l.0,08\times1000=80\\ m.3,14\times10=31,4\)

Ta có:

+) Vì \(\overline{2abb}⋮\) \(2\) và \(5\)nên:

\(b=0\)

+) Vì \(\overline{2abb}⋮3\) nên:

\(2+a+b+b=2+a+0+0=a+2⋮3\)

\(\Rightarrow\left(a+2\right)\in\left\{3,6,9\right\}\) (vì \(1\le a\le9\))

\(\Rightarrow a\in\left\{1,4,7\right\}\)

Vậy...

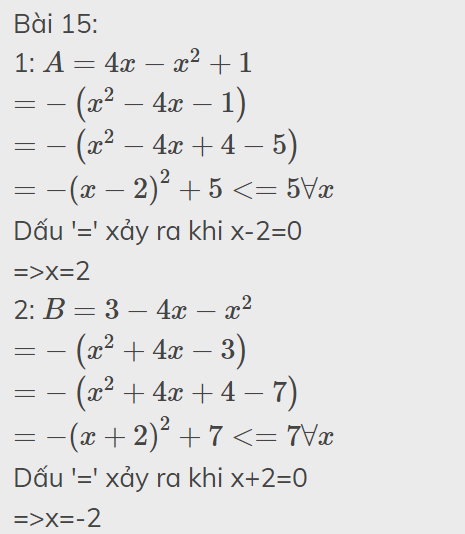
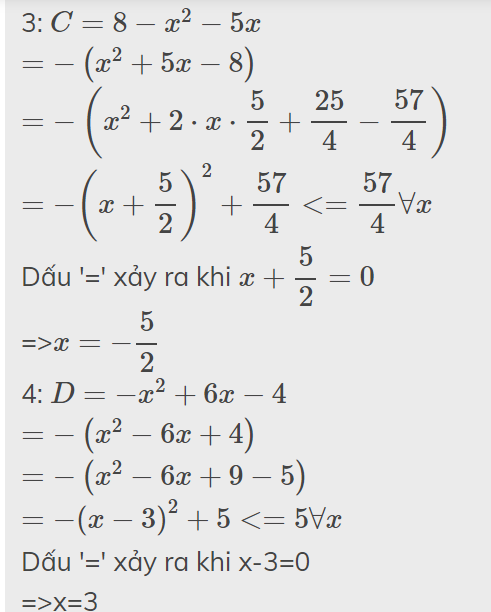
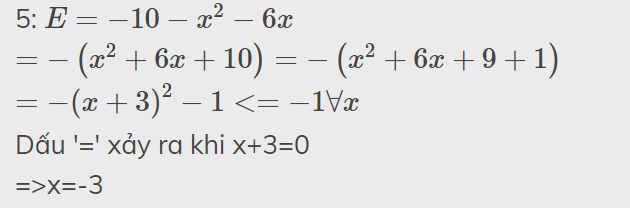
Bài 14:

1: \(A=x^2-x+3\)

\(=x^2-x+\dfrac{1}{4}+\dfrac{11}{4}\)

\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>=\dfrac{11}{4}\forall x\)

Dấu '=' xảy ra khi x-1/2=0

=>\(x=\dfrac{1}{2}\)

2: \(B=x^2+x+1\)

\(=x^2+x+\dfrac{1}{4}+\dfrac{3}{4}\)

\(=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall x\)

Dấu '=' xảy ra khi \(x+\dfrac{1}{2}=0\)

=>\(x=-\dfrac{1}{2}\)

3: \(C=x^2-4x+1\)

\(=x^2-4x+4-3\)

\(=\left(x-2\right)^2-3>=-3\forall x\)

Dấu '=' xảy ra khi x-2=0

=>x=2

4: \(D=x^2-5x+7\)

\(=x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{3}{4}\)

\(=\left(x-\dfrac{5}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall x\)

Dấu '=' xảy ra khi \(x-\dfrac{5}{2}=0\)

=>\(x=\dfrac{5}{2}\)

5: \(E=x^2+2x+2\)

\(=x^2+2x+1+1=\left(x+1\right)^2+1>=1\forall x\)

Dấu '=' xảy ra khi x+1=0

=>x=-1

6: \(F=x^2-3x+1\)
\(=x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}-\dfrac{5}{4}\)

\(=\left(x-\dfrac{3}{2}\right)^2-\dfrac{5}{4}>=-\dfrac{5}{4}\forall x\)

Dấu '=' xảy ra khi \(x-\dfrac{3}{2}=0\)

=>\(x=\dfrac{3}{2}\)

7: \(G=x^2+3x+3\)

\(=x^2+2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{3}{4}\)

\(=\left(x+\dfrac{3}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall x\)

Dấu '=' xảy ra khi x+3/2=0

=>x=-3/2

8: \(H=3x^2+3-5x\)

\(=3\left(x^2-\dfrac{5}{3}x+1\right)\)

\(=3\left(x^2-2\cdot x\cdot\dfrac{5}{6}+\dfrac{25}{36}+\dfrac{11}{36}\right)\)

\(=3\left(x-\dfrac{5}{6}\right)^2+\dfrac{11}{12}>=\dfrac{11}{12}\forall x\)

Dấu '=' xảy ra khi x-5/6=0

=>x=5/6

9: \(I=4x+2x^2+3\)

\(=2\left(x^2+2x+\dfrac{3}{2}\right)\)

\(=2\left(x^2+2x+1+\dfrac{1}{2}\right)\)

\(=2\left(x+1\right)^2+1>=1\forall x\)

Dấu '=' xảy ra khi x+1=0

=>x=-1

10: \(K=4x^2+3x+2\)

\(=\left(2x\right)^2+2\cdot2x\cdot\dfrac{3}{4}+\dfrac{9}{16}+\dfrac{23}{16}\)

\(=\left(2x+\dfrac{3}{4}\right)^2+\dfrac{23}{16}>=\dfrac{23}{16}\forall x\)

Dấu '=' xảy ra khi 2x+3/4=0

=>x=-3/8

11: M=(x-1)(x-3)+11

\(=x^2-4x+3+11=x^2-4x+14\)

\(=x^2-4x+4+10=\left(x-2\right)^2+10>=10\forall x\)

Dấu '=' xảy ra khi x-2=0

=>x=2

12: \(N=\left(x-3\right)^2+\left(x-2\right)^2\)

\(=x^2-6x+9+x^2-4x+4\)

\(=2x^2-10x+13\)

\(=2\left(x^2-5x+\dfrac{13}{2}\right)=2\left(x^2-5x+\dfrac{25}{4}+\dfrac{1}{4}\right)\)

\(=2\left(x-\dfrac{5}{2}\right)^2+\dfrac{1}{2}>=\dfrac{1}{2}\forall x\)

Dấu '=' xảy ra khi x-5/2=0

=>x=5/2

a: Xét ΔBAE và ΔBDE có

BA=BD

\(\widehat{ABE}=\widehat{DBE}\)

BE chung

Do đó: ΔBAE=ΔBDE

b: ΔBAE=ΔBDE

=>\(\widehat{BAE}=\widehat{BDE}\)

=>\(\widehat{BDE}=90^0\)

=>DE\(\perp\)BC tại D

XétΔBHF vuông tại H và ΔBHC vuông tại H có

BH chung

\(\widehat{HBF}=\widehat{HBC}\)

Do đó ΔBHF=ΔBHC

c: Xét ΔBFC có

BH,CA là các đường cao

BH cắt CA tại E

Do đó: E là trực tâm của ΔBFC
=>FE\(\perp\)BC

mà DE\(\perp\)BC

và FE,DE có điểm chung là E

nên F,E,D thẳng hàng

\(d.\dfrac{59-x}{41}+\dfrac{57-x}{43}=\dfrac{41-x}{59}+\dfrac{43-x}{57}\\ \left(\dfrac{59-x}{41}+1\right)+\left(\dfrac{57-x}{43}+1\right)=\left(\dfrac{41-x}{59}+1\right)+\left(\dfrac{43-x}{57}+1\right)\\ \dfrac{100-x}{41}+\dfrac{100-x}{43}=\dfrac{100-x}{59}+\dfrac{100-x}{57}\\ \left(100-x\right)\left(\dfrac{1}{41}+\dfrac{1}{43}-\dfrac{1}{59}-\dfrac{1}{57}\right)=0\\ 100-x=0\\ x=100\)

\(a.6,17\times0,01=0,0617\\ b.2,038:0,1=20,38\\ c.546\times0,001=0,546\\ d.0,72:0,001=720\\ e.4,126:0,01=412,6\\ f.578\times0,01=5,78\\ g.9,18:0,1=91,8\\ h.0,76\times0,1=0,076\\ i.4,376:0,001=4376\\ k.82,3\times0,001=0,0823\\ l.7,8\times0,1=0,78\\ m.13:0,1=130\)

GIÚP MIK ĐI MÌNH ĐANG GẤP ĐÓ MNG👉👈😱

bài 4:

\(C=\left(1+\dfrac{1}{1\cdot3}\right)\left(1+\dfrac{1}{2\cdot4}\right)\cdot...\cdot\left(1+\dfrac{1}{98\cdot100}\right)\)

\(=\left(1+\dfrac{1}{2^2-1}\right)\left(1+\dfrac{1}{3^2-1}\right)\cdot...\cdot\left(1+\dfrac{1}{99^2-1}\right)\)

\(=\dfrac{2^2}{2^2-1}\cdot\dfrac{3^2}{3^2-1}\cdot...\cdot\dfrac{99^2}{99^2-1}\)

\(=\dfrac{2\cdot3\cdot...\cdot99}{1\cdot2\cdot3\cdot...\cdot98}\cdot\dfrac{2\cdot3\cdot...\cdot99}{3\cdot4\cdot...\cdot100}=\dfrac{99}{1}\cdot\dfrac{2}{100}=\dfrac{99}{50}\)

Bài 5:

\(B=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{205}}{\dfrac{204}{1}+\dfrac{203}{2}+...+\dfrac{1}{204}}\)

\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{205}}{\left(1+\dfrac{203}{2}\right)+\left(1+\dfrac{202}{3}\right)+...+\left(\dfrac{1}{204}+1\right)+1}\)

\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{205}}{\dfrac{205}{2}+\dfrac{205}{3}+...+\dfrac{205}{205}}=\dfrac{1}{205}\)

a) 8 cm = 0,08 m

b) 0,52 m = 5,2 dm

c) 0,6 l = 600 ml

d) 84 g = 0,084 kg

e) 4 m² = 0,0004 ha

f) 0,178 ha = 1780 m²

g) 5,8 dam² = 580 m²

h) 956 cm² = 9,56 dm²

GIÚP MÌNH VỚI MỌI NGƯỜI!! mình rất bận:)))

Nhận thấy \(x_0=0\) không phải là nghiệm của phương trình đã cho.

Giả sử \(x_0< 0\), ta có \(x_0^3-x_0-1=0\) 

\(\Leftrightarrow x_0\left(x_0^2-1\right)=1\)

\(\Leftrightarrow x_0\left(x_0-1\right)\left(x_0+1\right)=1\)    (*)

Nếu \(x_0\le-1\) thì VT (*) \(\le0< 1=VP\), do đó (*) vô lý.

Xét \(-1< x_0< 0\) thì \(-1< x_0^3< 0\) và \(0< -x_0< 1\)

Do đó \(VT=x_0^3-x_0< 0+1=1=VP\) nên (*) vô lý.

Vậy điều giả sử ban đầu là sai \(\Rightarrow x_0>0\)

Đặt f(x)=x³-x-1

Vì \(f\left(x\right)=x^3-x-1\)

nên hàm số liên tục trên R

\(f\left(1\right)=1^3-1-1=-1;f\left(2\right)=2^3-2-1=5\)

Vì \(f\left(1\right)\cdot f\left(2\right)< 0\)

nên hàm số f(x)=x³-x-1 có nghiệm trên khoảng (1;2)

=>\(x_0\in\left(1;2\right)\)

=>\(x_0>0\)