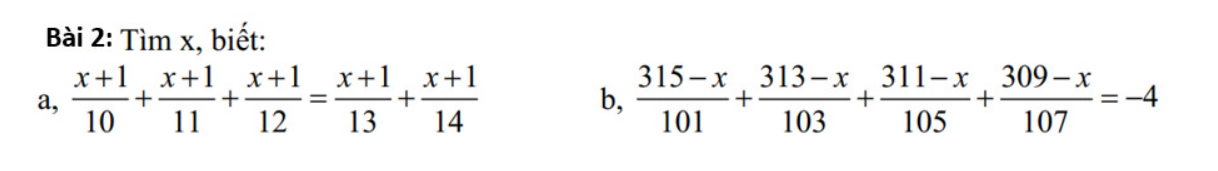 giải giúp tôi với ai giải được mình tick cho ai giải đc mình cảm ơn
giải giúp tôi với ai giải được mình tick cho ai giải đc mình cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hiệu số tuổi giữa tuổi cha và tuổi con là:
43-12=31(tuổi)
Ta có sơ đồ sau khi tuổi cha gấp tuổi con 2 lần
Tuổi cha 2 phần
Tuổi con 1 phần
Hiệu là 31t ở 1 phần còn lại
Hiệu số phần bằng nhau là :
2-1=1 phần
Gía trị 1 phần hay tuổi con lúc tuổi cha gấp đôi tuổi con là
31:1=31(tuổi)
Sau số năm thì tuổi cha gấp đôi tuổi con là:
31-12=19(năm)
Đ/S: 19 năm

Bài 8:
1: \(\dfrac{-20}{41}\cdot\dfrac{-4}{5}=\dfrac{20}{5}\cdot\dfrac{4}{41}=4\cdot\dfrac{4}{41}=\dfrac{16}{41}\)
2: \(\dfrac{-24}{5}\cdot\dfrac{15}{-8}=\dfrac{-24}{-8}\cdot\dfrac{15}{5}=3\cdot3=9\)
3: \(\dfrac{-4}{34}\cdot\dfrac{17}{-24}=\dfrac{4}{24}\cdot\dfrac{17}{34}=\dfrac{1}{2}\cdot\dfrac{1}{6}=\dfrac{1}{12}\)
Bài 6:
1: \(2\dfrac{3}{5}-1\dfrac{2}{3}=\dfrac{13}{5}-\dfrac{5}{3}=\dfrac{39}{15}-\dfrac{25}{15}=\dfrac{14}{15}\)
2: \(3\dfrac{3}{7}+2\dfrac{1}{2}=\dfrac{24}{7}+\dfrac{5}{2}=\dfrac{48}{14}+\dfrac{35}{14}=\dfrac{83}{14}\)
3: \(-3\dfrac{1}{2}-2\dfrac{1}{4}=\dfrac{-7}{2}-\dfrac{9}{4}=\dfrac{-14}{4}-\dfrac{9}{4}=-\dfrac{23}{4}\)
4: \(-2\dfrac{1}{2}-3\dfrac{1}{4}=-\dfrac{5}{2}-\dfrac{13}{4}=-\dfrac{10}{4}-\dfrac{13}{4}=-\dfrac{23}{4}\)
5: \(-4\dfrac{1}{2}+2\dfrac{3}{10}=-\dfrac{9}{2}+\dfrac{23}{10}=-\dfrac{45}{10}+\dfrac{23}{10}=-\dfrac{22}{10}=-\dfrac{11}{5}\)
6: \(-6\dfrac{1}{7}-\left(-7\dfrac{1}{6}\right)=-6-\dfrac{1}{7}+7+\dfrac{1}{6}\)
\(=1-\dfrac{1}{7}+\dfrac{1}{6}=\dfrac{6}{7}+\dfrac{1}{6}=\dfrac{43}{42}\)

Bài 7:
\(1)\dfrac{2}{7}+\dfrac{6}{21}-\dfrac{3}{14}\\ =\dfrac{12}{42}+\dfrac{12}{42}-\dfrac{12}{42}\\ =\dfrac{12}{42}\\ =\dfrac{2}{7}\\ 2)-\dfrac{7}{2}+\dfrac{3}{4}-\dfrac{17}{12}\\ =\dfrac{-42}{12}+\dfrac{9}{12}-\dfrac{17}{12}\\ =\dfrac{-50}{12}=\dfrac{-25}{6}\\ 3)\dfrac{1}{12}+\dfrac{1}{4}+\dfrac{2}{3}\\ =\dfrac{1}{12}+\dfrac{3}{12}+\dfrac{8}{12}=\dfrac{12}{12}=1\\ 4)\dfrac{1}{3}+\dfrac{-4}{5}-\dfrac{8}{15}\\ =\dfrac{5}{15}+\dfrac{-12}{15}-\dfrac{8}{15}=-\dfrac{15}{15}=-1\\ 5)\dfrac{2}{3}+\dfrac{-3}{4}+\dfrac{2}{6}\\ =\dfrac{2}{3}+\dfrac{-3}{4}+\dfrac{1}{3}\\ =\left(\dfrac{2}{3}+\dfrac{1}{3}\right)+\dfrac{-3}{4}\\ =1+\dfrac{-3}{4}\\ =\dfrac{1}{4}\\ 6\text{ })-\dfrac{5}{18}+\dfrac{5}{45}-\dfrac{9}{6}\\ =-\dfrac{5}{18}+\dfrac{1}{9}-\dfrac{3}{2}\\ =-\dfrac{5}{18}+\dfrac{2}{18}-\dfrac{27}{18}\\ =-\dfrac{30}{18}\\ =-\dfrac{5}{3}\)
Bài 8:
1: \(\dfrac{-20}{41}\cdot\dfrac{-4}{5}=\dfrac{20}{5}\cdot\dfrac{4}{41}=4\cdot\dfrac{4}{41}=\dfrac{16}{41}\)
2: \(\dfrac{-24}{5}\cdot\dfrac{15}{-8}=\dfrac{-24}{-8}\cdot\dfrac{15}{5}=3\cdot3=9\)
3: \(\dfrac{-4}{34}\cdot\dfrac{17}{-24}=\dfrac{4}{24}\cdot\dfrac{17}{34}=\dfrac{1}{2}\cdot\dfrac{1}{6}=\dfrac{1}{12}\)
Bài 6:
1: \(2\dfrac{3}{5}-1\dfrac{2}{3}=\dfrac{13}{5}-\dfrac{5}{3}=\dfrac{39}{15}-\dfrac{25}{15}=\dfrac{14}{15}\)
2: \(3\dfrac{3}{7}+2\dfrac{1}{2}=\dfrac{24}{7}+\dfrac{5}{2}=\dfrac{48}{14}+\dfrac{35}{14}=\dfrac{83}{14}\)
3: \(-3\dfrac{1}{2}-2\dfrac{1}{4}=\dfrac{-7}{2}-\dfrac{9}{4}=\dfrac{-14}{4}-\dfrac{9}{4}=-\dfrac{23}{4}\)
4: \(-2\dfrac{1}{2}-3\dfrac{1}{4}=-\dfrac{5}{2}-\dfrac{13}{4}=-\dfrac{10}{4}-\dfrac{13}{4}=-\dfrac{23}{4}\)
5: \(-4\dfrac{1}{2}+2\dfrac{3}{10}=-\dfrac{9}{2}+\dfrac{23}{10}=-\dfrac{45}{10}+\dfrac{23}{10}=-\dfrac{22}{10}=-\dfrac{11}{5}\)
6: \(-6\dfrac{1}{7}-\left(-7\dfrac{1}{6}\right)=-6-\dfrac{1}{7}+7+\dfrac{1}{6}\)
\(=1-\dfrac{1}{7}+\dfrac{1}{6}=\dfrac{6}{7}+\dfrac{1}{6}=\dfrac{43}{42}\)

a: Ta có: ΔOCK vuông tại C
=>\(CK^2+CO^2=OK^2\)
=>\(CK=\sqrt{10^2-8^2}=6\left(cm\right)\)
Xét ΔOCK vuông tại C có CA là đường cao
nên \(OA\cdot OK=OC^2;CA\cdot OK=CO\cdot CK\)
=>\(OA=\dfrac{OC^2}{OK}=\dfrac{8^2}{10}=6,4\left(cm\right);CA=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\)
Xét ΔCOK vuông tại C có \(sinCOK=\dfrac{CK}{OK}=\dfrac{6}{10}=\dfrac{3}{5}\)
nên \(\widehat{COK}=\widehat{xOy}\simeq36^052'\)
b: Xét ΔCAO vuông tại A có AH là đường cao
nên \(CH\cdot CO=CA^2\left(1\right)\)
Xét ΔCOK vuông tại O có CA là đường cao
nên \(AO\cdot AK=AC^2\left(2\right)\)
Từ (1),(2) suy ra \(CH\cdot CO=AO\cdot AK\)

Tớ sẽ làm mẫu cho cậu 1 số bài nhé:
a) \(A=\dfrac{6-5}{5.6}+\dfrac{7-6}{6.7}+...+\dfrac{25-24}{24.25}\)
\(A=\dfrac{6}{5.6}-\dfrac{5}{5.6}+\dfrac{7}{6.7}-\dfrac{6}{6.7}+...+\dfrac{25}{24.25}-\dfrac{24}{24.25}\)
\(A=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{24}-\dfrac{1}{25}\)
\(A=\dfrac{1}{5}-\dfrac{1}{25}\)
\(A=\dfrac{4}{25}\)
Bài 4; 2 và câu d bài 1 cậu sẽ cần phải đưa tử về hiệu giữa 2 thừa số ở mẫu.
\(\dfrac{4}{5}\) K = \(\dfrac{7-3}{3.7}+\dfrac{11-7}{7.11}+\dfrac{15-11}{11.15}=...+\dfrac{85-81}{81.85}+\dfrac{89-85}{85.89}\)
\(\dfrac{4}{5}K=\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{15}+...+\dfrac{1}{81}-\dfrac{1}{85}+\dfrac{1}{85}-\dfrac{1}{89}\)
\(\dfrac{4}{5}K=\dfrac{1}{3}-\dfrac{1}{89}\)
\(\dfrac{4}{5}K=\dfrac{43}{147}\)
\(K=\dfrac{43}{147}\div\dfrac{4}{5}\)
\(K=\dfrac{215}{588}\)
Với bài 3 thì cậu chỉ cần đảo vị trí từ dưới lên trên là được nhé.
Bài 5: (Viết lại tổng E). Khoảng cách giữa 2 thừa số ở mẫu là 6, cậu hãy nhân tử với 6, tính sau đó : 6 nhé.
→ E = \(\dfrac{1}{1.7}+\dfrac{1}{7.13}+\dfrac{1}{13.19}+\dfrac{1}{19.25}+\dfrac{1}{25.31}+\dfrac{1}{31.37}\)
\(C=\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+\dfrac{2}{9.11}+\dfrac{2}{11.13}\)
Bài 6. Quan sát:
\(3\left(\dfrac{1}{5}-\dfrac{3}{x-2}\right)=\dfrac{24}{35}\) và tương tự như câu b, luôn là cái đầu tiên - cái cuối cùng.
Bài 7. Cậu trừ 1 ở cả 2 vế rồi nhân \(\dfrac{1}{2}\).
\(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{x\left(x+1\right)}\)
= \(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{x\left(x+1\right)}\)
Cậu cứ làm như những bài trên nhé.
Bài 1:
\(a,A=\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{24.25}\)
\(=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{24}-\dfrac{1}{25}\)
\(=\dfrac{1}{5}-\dfrac{1}{25}=>\dfrac{5}{25}-\dfrac{1}{25}\)
\(=\dfrac{4}{25}\)
\(b,B=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{99.101}\)
\(=1.\left(\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{99.101}\right)\)
\(=1.\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)
\(=1.\left(1-\dfrac{1}{101}\right)\)
\(=\dfrac{100}{101}\)
\(c,K=\dfrac{4}{11.16}+\dfrac{4}{16.21}+\dfrac{4}{21.26}+...+\dfrac{4}{61.66}\)
\(=\dfrac{4}{5}.\left(\dfrac{1}{11.16}+\dfrac{1}{16.21}+\dfrac{1}{21.26}+...+\dfrac{1}{61.66}\right)\)
\(=\dfrac{4}{5}.\left(\dfrac{1}{11}-\dfrac{1}{16}+\dfrac{1}{16}-\dfrac{1}{21}+...+\dfrac{1}{61}-\dfrac{1}{66}\right)\)
\(=\dfrac{4}{5}.\left(\dfrac{1}{11}-\dfrac{1}{66}\right)\)
\(=\dfrac{4}{5}.\dfrac{5}{66}=>4.\dfrac{1}{66}\)
\(=\dfrac{4}{66}=\dfrac{2}{33}\)
\(d,N=\dfrac{4}{1.3}+\dfrac{4}{3.5}+\dfrac{4}{5.7}+...+\dfrac{4}{99.101}\)
\(=2.\left(\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{99.101}\right)\)
\(=2.\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)
\(=2.\left(1-\dfrac{1}{101}\right)\)
\(=2.\dfrac{100}{101}\)
\(=\dfrac{200}{101}\)
Bài 2:
\(K=\dfrac{5}{3.7}+\dfrac{5}{7.11}+\dfrac{5}{11.15}+...+\dfrac{5}{81.85}+\dfrac{5}{85.89}\)
\(=\dfrac{5}{4}.\left(\dfrac{1}{3.7}+\dfrac{1}{7.11}+\dfrac{1}{11.15}+...+\dfrac{1}{81.85}+\dfrac{1}{85.89}\right)\)
\(=\dfrac{5}{4}.\left(\dfrac{1}{3}-\dfrac{1}{7}+...+\dfrac{1}{85}-\dfrac{1}{89}\right)\)
\(=\dfrac{5}{4}.\left(\dfrac{1}{3}-\dfrac{1}{89}\right)\)
\(=\dfrac{5}{4}.\dfrac{86}{267}\)
\(=\dfrac{215}{534}\)
Bài 3:
\(A=\dfrac{1}{25.24}+\dfrac{1}{24.23}+...+\dfrac{1}{7.6}+\dfrac{1}{6.5}\)
\(=\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{23.24}+\dfrac{1}{24.25}\)
\(=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{24}-\dfrac{1}{25}\)
\(=\dfrac{1}{5}-\dfrac{1}{25}\)
\(=\dfrac{4}{25}\)
Bài 4 :
\(A=\dfrac{5}{3.6}+\dfrac{5}{6.9}+\dfrac{5}{9.12}+...+\dfrac{5}{99.102}\)
\(=\dfrac{5}{3}.\left(\dfrac{1}{3.6}+\dfrac{1}{6.9}+\dfrac{1}{9.12}+...+\dfrac{1}{99.102}\right)\)
\(=\dfrac{5}{3}.\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+...+\dfrac{1}{99}-\dfrac{1}{102}\right)\)
\(=\dfrac{5}{3}.\left(\dfrac{1}{3}-\dfrac{1}{102}\right)\)
\(=\dfrac{5}{3}.\dfrac{11}{34}\)
\(=\dfrac{55}{102}\)
Bài 5 :
Sửa đề :\(a,E=\dfrac{1}{7}+\dfrac{1}{91}+\dfrac{1}{247}+\dfrac{1}{475}+\dfrac{1}{775}+\dfrac{1}{1147}\)
\(=\dfrac{1}{1.7}+\dfrac{1}{7.13}+\dfrac{1}{13.19}+\dfrac{1}{19.25}+\dfrac{1}{25.31}+\dfrac{1}{31.37}\)
\(=\dfrac{1}{6}.\left(\dfrac{1}{1.7}+\dfrac{1}{7.13}+\dfrac{1}{13.19}+\dfrac{1}{19.25}+\dfrac{1}{25.31}+\dfrac{1}{31.37}\right)\)
\(=\dfrac{1}{6}.\left(1-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{13}+...+\dfrac{1}{31}-\dfrac{1}{37}\right)\)
\(=\dfrac{1}{6}.\left(1-\dfrac{1}{37}\right)\)
\(=\dfrac{1}{6}.\dfrac{36}{37}\)
\(=\dfrac{6}{37}\)
\(b,C=\dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+\dfrac{2}{99}+\dfrac{2}{143}\)
\(=\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+\dfrac{2}{9.11}+\dfrac{2}{11.13}\)
\(=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{11}-\dfrac{1}{13}\)
\(=\dfrac{1}{3}-\dfrac{1}{13}\)
\(=\dfrac{10}{39}\)
Bài 6 :
\(a,\dfrac{3}{5.7}+\dfrac{3}{7.9}+\dfrac{3}{9.11}+...+\dfrac{3}{x\left(x+2\right)}=\dfrac{24}{35}\)
\(\dfrac{3}{2}\left(\dfrac{2}{5.7}+\dfrac{2}{7.9}+\dfrac{2}{9.11}+...+\dfrac{2}{x\left(x+2\right)}\right)=\dfrac{24}{35}\)
\(\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{x+2}\right)=\dfrac{24}{35}\)
\(\dfrac{1}{5}-\dfrac{1}{x+2}=\dfrac{24}{35}:\dfrac{3}{2}\)
\(\dfrac{1}{5}-\dfrac{1}{x+2}=\dfrac{16}{35}\)
\(\dfrac{1}{x+2}=\dfrac{1}{5}-\dfrac{16}{35}\)
\(\dfrac{1}{x+2}=-\dfrac{9}{35}\)
\(-9\left(x+2\right)=1.35\)
\(-9\left(x+2\right)=35\)
\(x+2=35:-9\)
\(x+2=\dfrac{-35}{9}\)
\(x\) \(=\dfrac{-35}{9}-2\)
\(x\) \(=\dfrac{-53}{9}\)
Vậy \(x=\dfrac{-53}{9}\)
\(b,\dfrac{2}{4.7}+\dfrac{2}{7.10}+\dfrac{2}{10.13}+...+\dfrac{2}{x\left(x+3\right)}=\dfrac{1}{9}\)
\(\dfrac{2}{3}.\left(\dfrac{3}{4.7}+\dfrac{3}{7.10}+\dfrac{3}{10.13}+...+\dfrac{3}{x\left(x+3\right)}\right)=\dfrac{1}{9}\)
\(\dfrac{2}{3}.\left(\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{x}-\dfrac{1}{x+3}\right)=\dfrac{1}{9}\)
\(\dfrac{2}{3}.\left(\dfrac{1}{4}-\dfrac{1}{x+3}\right)\) \(=\dfrac{1}{9}\)
\(\dfrac{1}{6}-\dfrac{2}{3.\left(x+3\right)}\) \(=\dfrac{1}{9}\)
\(\dfrac{2}{3.\left(x+3\right)}\) \(=\dfrac{1}{6}-\dfrac{1}{9}\)
\(\dfrac{2}{3.\left(x+3\right)}\) \(=\dfrac{1}{18}\)
\(\dfrac{2}{3.\left(x+3\right)}\) \(=\dfrac{2}{36}\)
⇒ \(3.\left(x+3\right)=36\)
\(x+3=36:3\)
\(x+3=12\)
\(x\) \(=12-3\)
\(x\) \(=9\)
Vậy \(x=9\)
Bài 7:
\(1+\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+...+\dfrac{2}{x\left(x+1\right)}=1\dfrac{1989}{1991}\)
\(=>\dfrac{2}{2}+\dfrac{2}{6}+\dfrac{2}{12}+...+\dfrac{2}{x.\left(x+1\right)}=\dfrac{3980}{1991}\)
\(=>\dfrac{2}{1.2}+\dfrac{2}{2.3}+\dfrac{2}{3.4}+...+\dfrac{2}{x.\left(x+1\right)}=\dfrac{3980}{1991}\)
\(=>2.\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}...+\dfrac{1}{x.\left(x+1\right)}\right)=\dfrac{3980}{1991}\)
\(=>2.\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{x}-\dfrac{1}{x+1}\right)=\dfrac{3980}{1991}\)
\(=>2.\left(1-\dfrac{1}{x+1}\right)=\dfrac{3980}{1991}\)
\(1-\dfrac{1}{x+1}=\dfrac{3980}{1991}:2\)
\(1-\dfrac{1}{x+1}=\dfrac{1990}{1991}\)
\(\dfrac{1}{x+1}=1-\dfrac{1990}{1991}\)
\(\dfrac{1}{x+1}=\dfrac{1}{1991}\)
\(=>x+1=1991\)
\(x\) \(=1991-1\)
\(x\) \(=1990\)
Vậy \(x=1990\)

1.
$2(x^2-4x+4)=(x-2)(x+3)$
$\Leftrightarrow 2(x-2)^2=(x-2)(x+3)$
$\Leftrightarrow 2(x-2)^2-(x-2)(x+3)=0$
$\Leftrightarrow (x-2)[2(x-2)-(x+3)]=0$
$\Leftrightarrow (x-2)(x-7)=0$
$\Leftrightarrow x-2=0$ hoặc $x-7=0$
$\Leftrightarrow x=2$ hoặc $x=7$
2.
$4x^2=9$
$\Leftrightarrow (2x)^2-3^2=0$
$\Leftrightarrow (2x-3)(2x+3)=0$
$\Leftrightarrow 2x-3=0$ hoặc $2x+3=0$
$\Leftrightarrow x=\frac{3}{2}$ hoặc $x=\frac{-3}{2}$
3.
$9x^2-1=(3x+1)(x+2)$
$\Leftrightarrow (3x+1)(3x-1)=(3x+1)(x+2)$
$\Leftrightarrow (3x+1)(3x-1)-(3x+1)(x+2)=0$
$\Leftrightarrow (3x+1)(3x-1-x-2)=0$
$\Leftrightarrow (3x+1)(2x-3)=0$
$\Leftrightarrow 3x+1=0$ hoặc $2x-3=0$
$\Leftrightarrow x=\frac{-1}{3}$ hoặc $x=\frac{3}{2}$

Bạn lưu ý, khi đăng đề thì đăng đầy đủ đề (bao gồm cả điều kiện và yêu cầu).
Đề yêu cầu tìm $x,y$?
$x,y$ là số như thế nào? Số nguyên? Số tự nhiên?
Bạn nên ghi rõ ra để mọi người hỗ trợ nhanh hơn nhé.
\(x+2xy-2y=5\)
\(x+2y\times\left(x-1\right)=5\)
\(\left(x-1\right)+2y\times\left(x-1\right)=5-1\)
\(\left(x-1\right)\times\left(2y+1\right)=4\)
Ta có: 4 = (-1) x (-4) = (-2) x (-2) = 2 x 2 = 1 x 4
Ta lập bảng:
| x - 1 | 1 | -1 | 2 | -2 | 4 | -4 |
| x | 2 | 0 | 3 | -1 | 5 | -3 |
| 2y + 1 | 4 | -4 | 2 | -2 | 1 | -1 |
| y | X | X | X | X | 0 | -1 |
⇒ (x; y) ϵ {(5; 0); (-3; -1)}

\(\dfrac{3}{x}+\dfrac{4}{x-1}=\dfrac{5x-2}{x^2-x}\left(x\notin\left\{0;1\right\}\right)\\ \Leftrightarrow\dfrac{3\left(x-1\right)}{x\left(x-1\right)}+\dfrac{4x}{x\left(x-1\right)}=\dfrac{5x-1}{x\left(x-1\right)}\\ \Leftrightarrow3\left(x-1\right)+4x=5x-1\\ \Leftrightarrow3x-3+4x=5x-1\\ \Leftrightarrow7x-3=5x+1\\ \Leftrightarrow7x-5x=1+3\\ \Leftrightarrow2x=4\\ \Leftrightarrow x=\dfrac{4}{2}\\ \Leftrightarrow x=2\left(tm\right)\)







a)
\(\dfrac{x+1}{10}+\dfrac{x+1}{11}+\dfrac{x+1}{12}=\dfrac{x+1}{13}+\dfrac{x+1}{14}\\ \Rightarrow\dfrac{x+1}{10}+\dfrac{x+1}{11}+\dfrac{x+1}{12}-\dfrac{x+1}{13}-\dfrac{x+1}{14}=0\\ \Rightarrow\left(x+1\right)\cdot\left(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}-\dfrac{1}{13}-\dfrac{1}{14}\right)=0\)
Vì \(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}-\dfrac{1}{13}-\dfrac{1}{14}\ne0\) nên:
\(x+1=0\\ \Rightarrow x=-1\)
Vậy...
b) \(\dfrac{315-x}{101}+\dfrac{313-x}{103}+\dfrac{311-x}{105}+\dfrac{309-x}{107}=-4\\ \Rightarrow\dfrac{315-x}{101}+\dfrac{313-x}{103}+\dfrac{311-x}{105}+\dfrac{309-x}{107}+4=0\\ \Rightarrow\left(\dfrac{315-x}{101}+1\right)+\left(\dfrac{313-x}{103}+1\right)+\left(\dfrac{311-x}{105}+1\right)+\left(\dfrac{309-x}{107}+1\right)=0\\ \Rightarrow\dfrac{416-x}{101}+\dfrac{416-x}{103}+\dfrac{416-x}{105}+\dfrac{416-x}{107}=0\\ \Rightarrow\left(416-x\right)\left(\dfrac{1}{101}+\dfrac{1}{103}+\dfrac{1}{105}+\dfrac{1}{107}\right)=0\)
Vì \(\dfrac{1}{101}+\dfrac{1}{103}+\dfrac{1}{105}+\dfrac{1}{107}\ne0\) nên:
\(416-x=0\\ \Rightarrow x=416\)
Vậy...