Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = \(\dfrac{\dfrac{2022}{1}+\dfrac{2021}{2}+\dfrac{2020}{3}+...+\dfrac{1}{2022}}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2023}}\)
Xét TS = \(\dfrac{2022}{1}\) + \(\dfrac{2021}{2}\) \(\dfrac{2020}{3}\) +... + \(\dfrac{1}{2022}\)
TS = (1 + \(\dfrac{2021}{2}\)) + (1 + \(\dfrac{2020}{3}\)) + ... + ( 1 + \(\dfrac{1}{2022}\)) + 1
TS = \(\dfrac{2023}{2}\) + \(\dfrac{2023}{3}\) +...+ \(\dfrac{2023}{2022}\) + \(\dfrac{2023}{2023}\)
TS = 2023.(\(\dfrac{1}{2}\) + \(\dfrac{1}{3}\) + \(\dfrac{1}{4}\) +...+ \(\dfrac{1}{2023}\))
A = \(\dfrac{2023.\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2023}\right)}{\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2023}\right)}\)
A = 2023

Lời giải:
a. Thể tích cái bánh: $6\times 8\times 3:2=72$ (cm3)
b.
Độ dài cạnh chéo miếng bánh: $\sqrt{6^2+8^2}=10$ (cm)
Diện tích vật liệu cần dùng chính là diện tích toàn phần của cái bánh và bằng:
$6.8+6.3+3.8+10.3=120$ (cm2)

`#3107.101107`
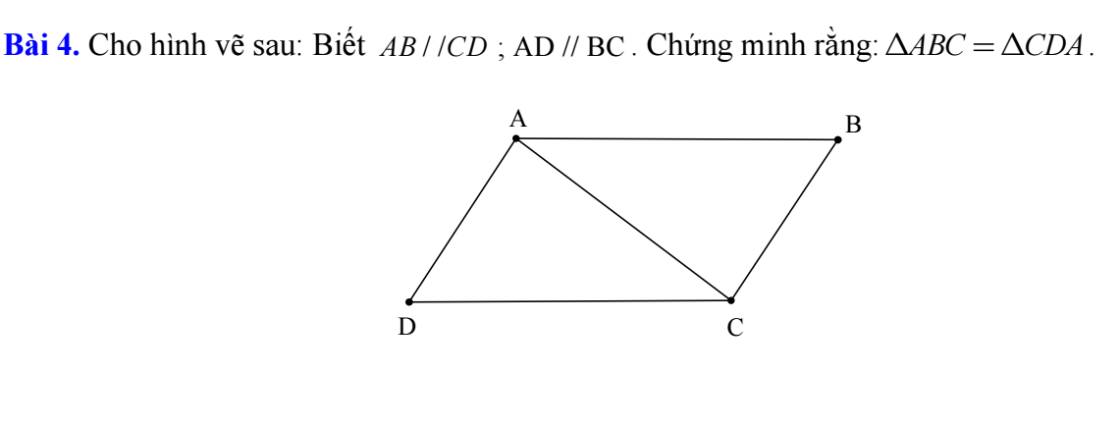
Ta có: `\text{AB // CD}`
\(\Rightarrow\) \(\widehat{\text{BAC}}=\widehat{\text{DCA}}\)
Vì `\text{AD // BC}`
\(\Rightarrow\widehat{\text{DAC}}=\widehat{\text{BCA}}\)
Xét `\Delta ABC` và `\Delta CDA` :
\(\widehat{\text{BAC}}=\widehat{\text{DCA}}\)
\(\text{AC chung}\)
\(\widehat{\text{DAC}}=\widehat{\text{BCA}}\)
\(\Rightarrow\Delta\text{ABC = }\Delta\text{CDA (g - c - g).}\)

Bài 3: 28 mét dây nặng số ki-lô-gam là:
0,5 x 28 : 4 = 3,5 (kg)
Kết luận: 28 mét dây nặng 3,5 kg

Ta có: \(5x=8y\)
hay \(\dfrac{x}{8}=\dfrac{y}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{8}=\dfrac{y}{5}=\dfrac{y-x}{5-8}=\dfrac{-15}{-3}=5\)
Do đó:
\(\dfrac{x}{8}=5\Rightarrow x=8.5=40\)
\(\dfrac{y}{5}=5\Rightarrow y=5.5=25\)
Vậy \(x=40\); \(y=25\)
Ta có 5x = 8y
hay x/8 = y/5
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
x/8 = y/5 = y-x/5-8 = -15/-3=5
do đó:
x/8 = 5 suy ra x = 8,5 = 40
y/5 = 5 suy ra y = 5,5 = 25
Vậy x = 40, y = 25

\(\dfrac{x-3}{5-x}\) = \(\dfrac{5}{7}\) (đk \(x\) ≠ 5)
7.(\(x\) - 3) = 5.(5 - \(x\))
7\(x\) - 21 = 25 - 5\(x\)
7\(x\) + 5\(x\) = 25 + 21
12\(x\) = 46
\(x\) = 46 : 12
\(x\) = \(\dfrac{23}{6}\)
\(\dfrac{\left|x-2\right|}{2}\) = \(\dfrac{\left|2x+3\right|}{3}\)
3.|\(x\) - 2| = |2\(x\) + 3|.2
lập bảng ta có:
| \(x\) | - \(\dfrac{3}{2}\) 2 |
| 3.|\(x\) -2| | -3\(x\) + 6 3\(x\) - 6 0 3\(x\) - 6 |
| |2\(x\) + 3|.2 | -4\(x\) - 6 0 -4\(x\) - 6 0 4\(x\) + 6 |
Theo bảng trên ta có:
\(x\) < - \(\dfrac{3}{2}\) ⇒ -3\(x\) + 6 = - 4\(x\) - 6
-\(3x\) + 4\(x\) = - 6 - 6
\(x\) = -12
- \(\dfrac{3}{2}\) < \(x\) < 2 ⇒ 3\(x\) - 6 = - 4\(x\) - 6
3\(x\) + 4\(x\) = 6 - 6
7\(x\) = 0
\(x\) = 0
2 < \(x\) ⇒ 3\(x\)- 6 = 4\(x\) + 6
4\(x\) - 3\(x\) = - 6 - 6
\(x\) = -12 (loại)
Vậy \(x\) \(\in\) {-12; 0}


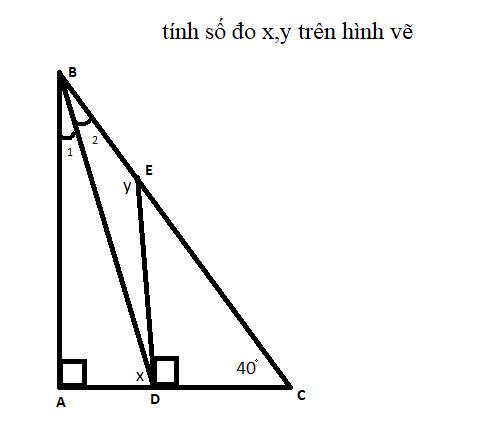
∆ABC có:
∠A + ∠ABC + ∠C = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠ABC = 180⁰ - (∠A + ∠C)
= 180⁰ - (90⁰ + 40⁰)
= 180⁰ - 130⁰
= 50⁰
⇒ ∠B₁ = ∠B₂ = 50⁰ : 2 = 25⁰
∆ABD có:
∠A + ∠B₁ + ∠ADB = 180⁰ (tổng ba góc trong ∆ABD)
⇒ x = ∠ADB = 180⁰ - (∠A + ∠B₁)
= 180⁰ - (90⁰ + 25⁰)
= 65⁰
⇒ ∠BDE = 90⁰ - ∠ADB
= 90⁰ - 65⁰
= 25⁰
∆BDE có:
∠B₂ + ∠BDE + ∠BED = 180⁰ (tổng ba góc trong ∆BDE)
⇒ y = ∠BED = 180⁰ - (∠B₂ + ∠BDE)
= 180⁰ - (25⁰ + 25⁰)
= 130⁰