Giúp me vs ah. Gia đình Hà muốn mua 1 căn nhà ở trung tâm tp Hà Tĩnh để thuận tiện cho việc mua sắm, đi học của con, và khám bệnh khi cần thiết sao cho khoảng cách từ căn nhà đó đến siêu thị, bệnh viện, trường học đều bằng nhau. Hãy giúp Hà xác định vị trí căn nhà cần mua ở đâu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) 1/2 x³.(4x² - 5x + 7)
= 2x⁵ - 5x⁴/2 + 7x³/2
b) (8x³ - 1) : (4x² + 2x + 1)
= (2x - 1)(4x² + 2x + 1) : (4x² + 2x + 1)
= 2x - 1
c) (2x - 4)(2x + 4)
= (2x)² - 4²
= 4x² - 16
d) (25y³ - 20y⁴ + 7y²) : (-5y²)
= -5y + 4y² - 7/5

Lời giải:
b.
$(x-1)(x+2)-(x+1)(x-3)-3x=1$
$\Leftrightarrow (x^2+x-2)-(x^2-2x-3)-3x=1$
$\Leftrightarrow x^2+x-2-x^2+2x+3-3x=1$
$\Leftrightarrow 0=0$ (luôn đúng)
Vậy PT có nghiệm $x$ là số thực bất kỳ
c.
$(3x+7)(2x+3)-(3x-5)(2x+11)=0$
$\Leftrightarrow (6x^2+23x+21)-(6x^2+23x-55)=0$
$\Leftrightarrow 76=0$ (vô lý)
Vậy không tồn tại $x$ thỏa mãn đề.

Lời giải:
$x^3-(x-2)(x^2+x-1)=4(x^2-2)$
$\Leftrightarrow x^3-(x^3+x^2-x-2x^2-2x+2)=4x^2-8$
$\Leftrightarrow x^3-(x^3-x^2-3x+2)=4x^2-8$
$\Leftrightarrow x^3-x^3+x^2+3x-2=4x^2-8$
$\Leftrightarrow x^2+3x-2=4x^2-8$
$\Leftrightarrow 3x^2-3x-6=0$
$\Leftrightarrow x^2-x-2=0$
$\Leftrightarrow (x+1)(x-2)=0$
$\Rightarrow x+1=0$ hoặc $x-2=0$
$\Rightarrow x=-1$ hoặc $x=2$

Lời giải:
1.
$A=3(x-3)+5-2(x-1)=3x-9+5-2x+2=(3x-2x)+(-9+5+2)=x-2=0$
$\Rightarrow x=2$
Vậy $x=2$ là nghiệm của đa thức.
2.
$B=x^2(3x+2)-2x(x-2)=3x^3+2x^2-2x^2+4x=3x^3+4x=x(3x^2+4)=0$
$\Rightarrow x=0$ hoặc $3x^2+4=0$
Nếu $3x^2+4=0$
$\Rightarrow 3x^2=-4<0$ (vô lý)
$\Rightarrow x=0$
Vậy $x=0$ là nghiệm của $B$
3.
$C=x^3+3x(x-2)-x(3x-7)=x^3+3x^2-6x-3x^2+7x=x^3+x=x(x^2+1)=0$
$\Rightarrow x=0$ hoặc $x^2+1=0$
Nếu $x^2+1=0$
$\Rightarrow x^2=-1<0$ (vô lý)
$\Rightarrow x=0$
Vậy $x=0$ là nghiệm duy nhất của $C$.

Lời giải:
a.
Tam giác $ABC$ vuông tại $B$ nên $\widehat{ABC}=90^0$
Xét tam giác $ABC$ có:
$\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0$ (tổng 3 góc trong 1 tam giác)
$\Rightarrow 90^0+30^0+\widehat{BAC}=180^0$
$\Rightarrow \widehat{BAC}=60^0$
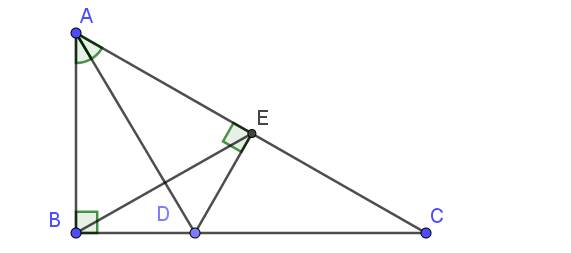
b.
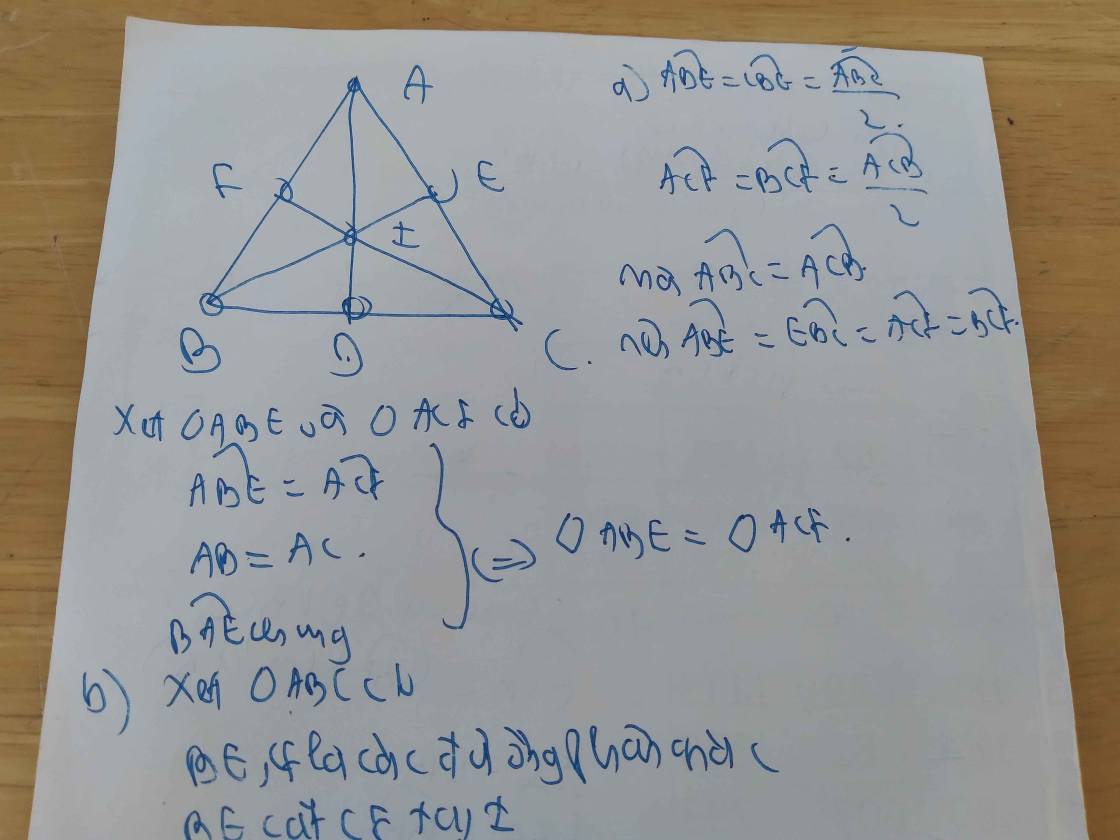
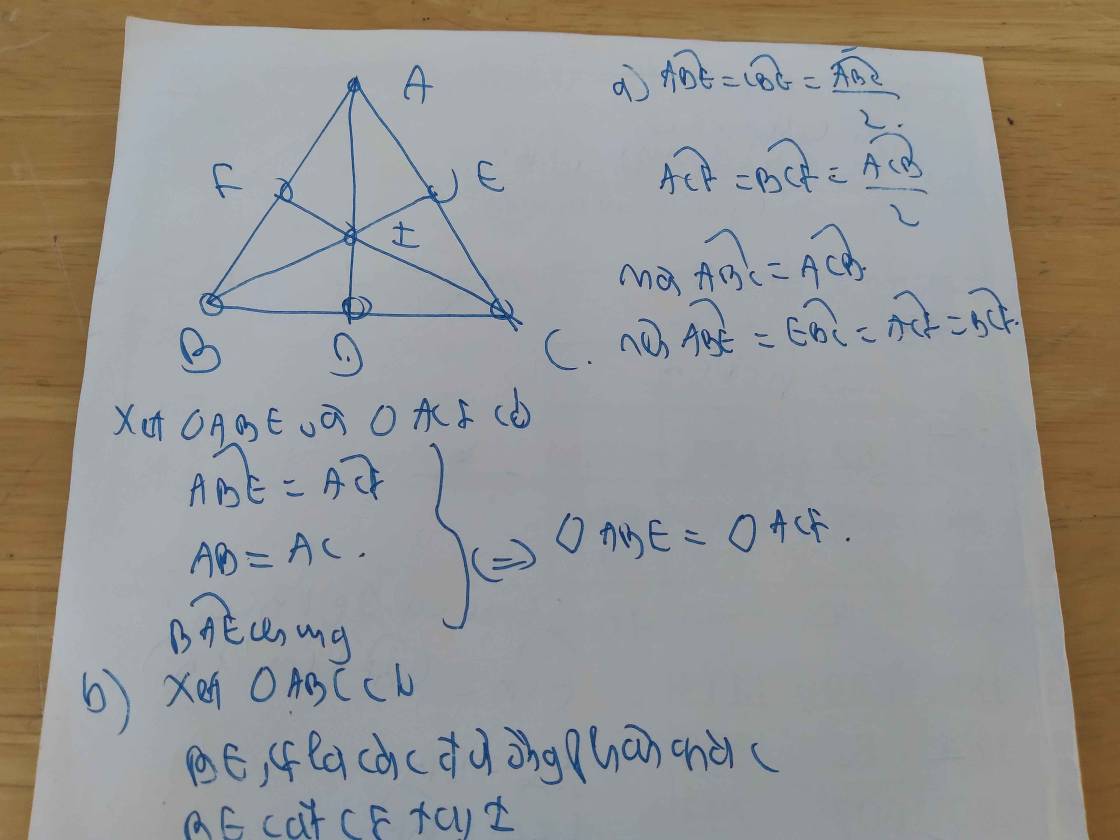
Xét tam giác $BAD$ và $EAD$ có:
$AD$ chung
$\widehat{BAD}=\widehat{EAD}$ (do $AD$ là phân giác $\widehat{A}$)
$\widehat{ABD}=\widehat{AED}=90^0$
$\Rightarrow \triangle BAD=\triangle EAD$ (ch-gn)
c.
Từ tam giác bằng nhau phần b suy ra $AB=AE$
$\Rightarrow ABE$ cân tại $A$
$\Rightarrow \widehat{ABE}=\widehat{AEB}$
Mà $\widehat{BAE}=60^0$ (kết quả phần a) nên:
$\widehat{ABE}=\widehat{AEB}=(180^0-\widehat{BAE}):2=(180^0-60^0):2=60^0$
Vậy $\widehat{ABE}=\widehat{AEB}=\widehat{BAE}=60^0$ nên $ABE$ là tam giác đều.




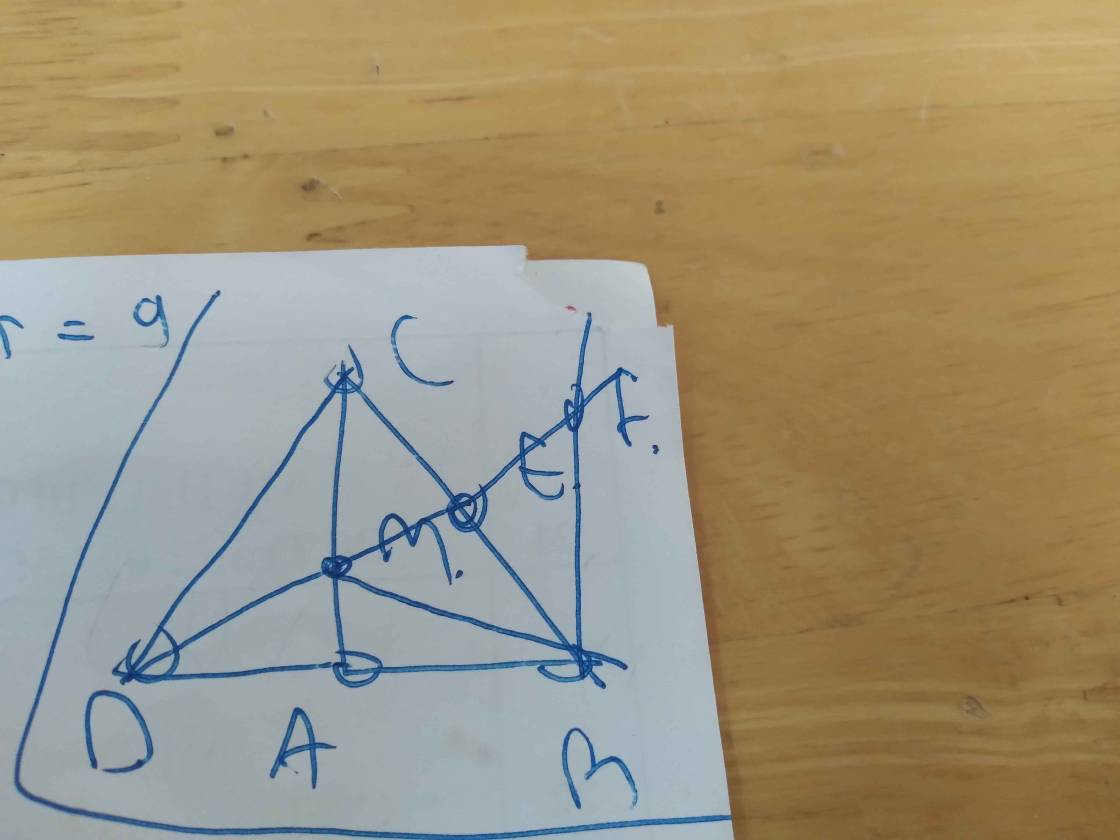













Để khoảng cách từ vị trí của nhà Hà đến siêu thị, bệnh viện, trường học đều bằng nhau thì nhà Hà nằm ở vị trí D là giao điểm của ba đường trung trực của ∆ABC như hình vẽ.
Siêu thị, bệnh viện, trường học nằm ở ba vị trí là ba đỉnh của ∆ABC