
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Chú ý rằng với hai người \(A\)và \(B\)thi đấu với nhau thì \(A\)thi đấu với \(B\)và \(B\)thi đấu với \(A\).
Mỗi người sẽ đấu với \(n-1\)người, nên tổng số ván đấu của giải là:
\(\frac{n\left(n-1\right)}{2}\).
b) Giả sử \(n=12\).
Tổng số ván đấu của giải là: \(\frac{12.11}{2}=66\).
Tổng số điểm của tất cả các kì thủ là: \(2\times66=132\).
Kì thủ cuối thắng ba kì thủ đứng đầu, do đó số điểm kì thủ cuối ít nhất là \(2.3=6\).
Do số điểm các kì thủ đôi một khác nhau nên tổng số điểm tối thiểu của tất cả các kì thủ là:
\(6+7+8+9+10+11+12+13+14+15+16+17=138>132\).
Do đó không thể xảy ra điều này.
Ta có đpcm.

đk: \(\orbr{\begin{cases}x\ge3\\x\le-2\end{cases}}\)
Ta có: \(\sqrt{x\left(x+1\right)}+\sqrt{x\left(x+2\right)}=\sqrt{x\left(x-3\right)}\)
\(\Leftrightarrow2x^2+3x+2\sqrt{x^2\left(x^2+3x+2\right)}=x^2-3x\)
\(\Leftrightarrow x^2+6x=-2\sqrt{x^2\left(x^2+3x+2\right)}\)
\(\Rightarrow x^4+12x^3+36x^2=4\left(x^4+3x^3+2x^2\right)\)
\(\Leftrightarrow3x^4-28x^2=0\)
\(\Leftrightarrow x^2\left(3x^2-28\right)=0\Rightarrow x\in\left\{0;\pm\frac{2\sqrt{21}}{3}\right\}\)
Thử lại thấy \(\orbr{\begin{cases}x=0\\x=-\frac{2\sqrt{21}}{3}\end{cases}}\) thỏa mãn
Vậy ...

Tâm đường tròn \(\left(C\right)\)là \(I\left(2,1\right)\).
\(\left(d'\right)\perp\left(d\right):2x+y+m=0\Rightarrow VTCP\overrightarrow{u_{d'}}=\left(2,1\right)\).
Đường thẳng \(\left(d'\right):\hept{\begin{cases}quaI\left(2,1\right)\\VTCP\overrightarrow{u_{d'}}=\left(2,1\right)\end{cases}}\)
Suy ra \(\left(d'\right):\left(x-2\right)-2\left(y-1\right)=0\Leftrightarrow x-2y=0\).

Nếu đề là giải phương trình. Bài này có cách giải cơ bản như sau:
\(3sin^2x-\frac{1}{2}sin2x+2cos^2x=0\)
\(\Leftrightarrow3sin^2x-sinxcosx+2cos^2x=0\)
- \(cosx=0\)khi đó \(sin^2x=1\)suy ra \(3sin^2x-sinxcosx+2cos^2x=3\)không thỏa.
- \(cosx\ne0\): phương trình tương đương với:
\(3\left(\frac{sinx}{cosx}\right)^2-\frac{sinx}{cosx}+2=0\)
\(\Leftrightarrow3tan^2x-tanx+2=0\)
\(\Delta=1-4.2.3< 0\)nên phương trình vô nghiệm.

ĐKXĐ bạn tự tìm nhé.
\(\sqrt{x\left(x+1\right)}+\sqrt{x\left(x+2\right)}=\sqrt{x\left(x-3\right)}\)
\(\Rightarrow\orbr{\begin{cases}\sqrt{x}=0\\\sqrt{x+1}+\sqrt{x+2}=\sqrt{x-3}\left(1\right)\end{cases}}\)
Bình phương hai vế của \(\left(1\right)\)ta được:
\(2x+3+2\sqrt{\left(x+1\right)\left(x+2\right)}=x-3\)
\(\Leftrightarrow-6-x=2\sqrt{\left(x+1\right)\left(x+2\right)}\)
\(\Rightarrow x^2+12x+36=4\left(x+1\right)\left(x+2\right)\)
\(\Leftrightarrow3x^2-28=0\)
\(\Leftrightarrow x=\pm\frac{2\sqrt{21}}{3}\).
Thử lại các nghiệm ta được \(x=0\)và \(x=-\frac{2\sqrt{21}}{3}\)thỏa mãn.
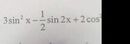
\(\frac{tan2x-tanx}{tan2xtanx}=\frac{1}{tanx}-\frac{1}{tan2x}=\frac{1}{tanx}-\frac{1-tan^2x}{2tanx}=\frac{1+tan^2x}{2tanx}=\frac{1+\frac{sin^2x}{cos^2x}}{\frac{2sinx}{cosx}}\)
\(=\frac{1}{2cosxsinx}=\frac{1}{sin2x}\)
suy ra \(\frac{tan2xtanx}{tan2x-tanx}=sin2x\).