\(\left(\dfrac{1}{2}\right)^x+\left(\dfrac{1}{2}\right)^{x+2}=\dfrac{1}{128}\\ \left(\dfrac{1}{2}\right)^x.\left[1+\left(\dfrac{1}{2}\right)^2\right]=\dfrac{1}{128}\\ \left(\dfrac{1}{2}\right)^x.\dfrac{5}{4}=\dfrac{1}{128}\\ \left(\dfrac{1}{2}\right)^x=\dfrac{1}{128}:\dfrac{5}{4}=\dfrac{1}{128}.\dfrac{4}{5}=\dfrac{4}{640}=\dfrac{1}{160}\)

Thầy thấy số lẻ quá....

`#3107.101107`

\(\left(\dfrac{1}{2}\right)^x+\left(\dfrac{1}{2}\right)^{x+2}=\dfrac{1}{128}\)

\(\Rightarrow\left(\dfrac{1}{2}\right)^x\cdot\left[1+\left(\dfrac{1}{2}\right)^2\right]=\dfrac{1}{128}\)

\(\Rightarrow\left(\dfrac{1}{2}\right)^x\cdot\left(1+\dfrac{1}{4}\right)=\dfrac{1}{128}\)

\(\Rightarrow\left(\dfrac{1}{2}\right)^x\cdot\dfrac{5}{4}=\dfrac{1}{128}\)

\(\Rightarrow\left(\dfrac{1}{2}\right)^x=\dfrac{1}{128}\div\dfrac{5}{4}\)

\(\Rightarrow\left(\dfrac{1}{2}\right)^x=\dfrac{1}{160}\)

Bạn xem lại đề.

Ta có: \(\left\{{}\begin{matrix}\left|0,25x-1\right|\ge0\forall x\\\left|3-2y\right|\ge0\forall y\end{matrix}\right.\)

\(\Rightarrow\left|0,25x-1\right|+\left|3-2y\right|\ge0\forall x,y\)

Mà: \(\left|0,25x-1\right|+\left|3-2y\right|=0\)

nên: \(\left\{{}\begin{matrix}0,25x-1=0\\3-2y=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}0,25x=1\\2y=3\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=4\\y=\dfrac{3}{2}\end{matrix}\right.\)

Vậy: \(x=4;y=\dfrac{3}{2}\).

A = 567383File: undefined 

Đổi 0,8 = 8/10 = 4/5

Hiệu số phần bằng nhau là:

5 - 4 = 1 (phần)

Số cây lớp 7a trồng là:

20 : 1 . 4 = 80 (cây)

Số cây lớp 7b trồng là:

80 + 20 = 100 (cây)

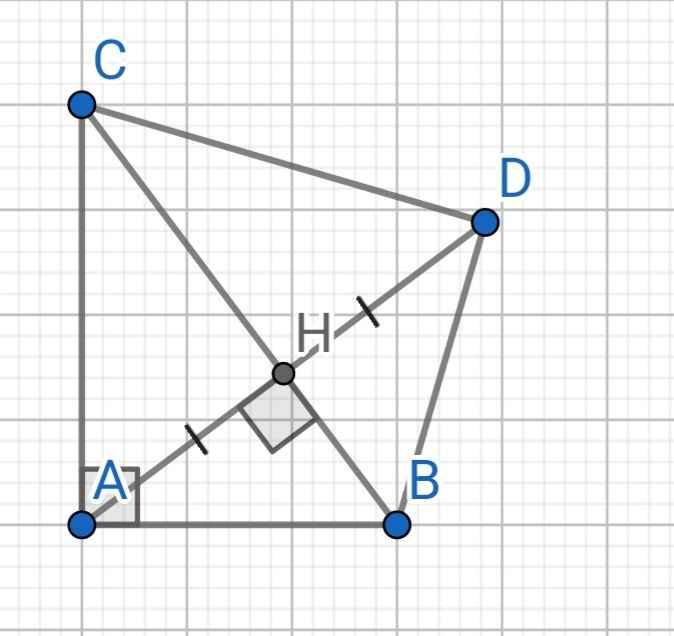 a) Xét hai tam giác vuông: ∆ABH và ∆DBH có:

BH là cạnh chung

HA = HD (gt)

⇒ ∆ABH = ∆DBH (hai cạnh góc vuông)

⇒ ∠ABH = ∠DBH (hai góc tương ứng)

⇒ BH là tia phân giác của ∠ABD

b) Do ∆ABH = ∆DBH (cmt)

⇒ AB = DB (hai cạnh tương ứng)

Do ∠ABH = ∠DBH (cmt)

⇒ ∠ABC = ∠DBC

Xét ∆ABC và ∆DBC có:

AB = DB (cmt)

∠ABC = ∠DBC (cmt)

AC là cạnh chung

⇒ ∆ABC = ∆DBC (c-g-c)

c) Do ∆ABC = ∆DBC (cmt)

⇒ ∠BAC = ∠BDC = 90⁰ (hai góc tương ứng)

⇒ BD ⊥ CD

Lời giải:
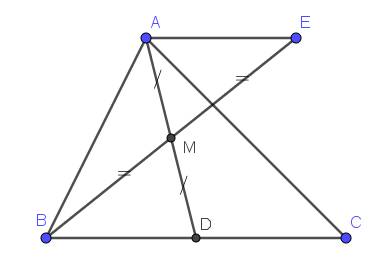
Xét tam giác $BMD$ và $EMA$ có:

$\widehat{BMD}=\widehat{EMA}$ (đối đỉnh) 

$BM=EM$ (gt) 

$MD=MA$ (do $M$ là trung điểm $AD$)

$\Rightarrow \triangle BMD=\triangle EMA$ (c.g.c)

$\Rightarrow BD=EA$ (đpcm)

và $\widehat{MBD}=\widehat{MEA}$

Mà 2 góc này ở vị trí so le trong nên $AE\parallel BD$ (đpcm)

Hình vẽ:

- \(\dfrac{1}{3}\) + \(\dfrac{1}{4}\)\(x\) = 0.2

            \(\dfrac{1}{4}\)\(x\) = \(\dfrac{1}{3}\) + 0

                \(x\) = \(\dfrac{1}{3}\) : \(\dfrac{1}{4}\)

                \(x\) = \(\dfrac{4}{3}\)