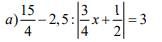Cô Hoài trả lời tin nhắn em với ạ!

a, \(\dfrac{15}{4}\) - 2,5 : |\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 3

    3,75 - 2,5:|\(\dfrac{3}{4}\)\(x\) +  \(\dfrac{1}{2}\)| = 3

             2,5:|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)|  = 3,75 - 3

            2,5 : |\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 0,75

                    |\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 2,5 : 0,75

                   |\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = \(\dfrac{10}{3}\)

                   \(\left[{}\begin{matrix}\dfrac{3}{4}x+\dfrac{1}{2}=-\dfrac{10}{3}\\\dfrac{3}{4}x+\dfrac{1}{2}=\dfrac{10}{3}\end{matrix}\right.\)

                  \(\left[{}\begin{matrix}\dfrac{3}{4}x=-\dfrac{10}{3}-\dfrac{1}{2}\\\dfrac{3}{4}x=\dfrac{10}{3}-\dfrac{1}{2}\end{matrix}\right.\)

                    \(\left[{}\begin{matrix}\dfrac{3}{4}x=-\dfrac{26}{3}\\\dfrac{3}{4}x=\dfrac{17}{6}\end{matrix}\right.\)

                      \(\left[{}\begin{matrix}x=-\dfrac{46}{9}\\x=\dfrac{34}{9}\end{matrix}\right.\)

AD = DB 

DE // BC 

⇒ E là trung điểm của AC (đpcm)

Vì một đường thẳng đi qua trung điểm của một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba

√(x + 1)² = 6

|x + 1| = 6

*) Với x ≥ -1, ta có:

x + 1 = 6

x = 6 - 1

x = 5 (nhận)

*) Với x < -1, ta có:

x + 1 = -6

x = -6 - 1

x = -7 (nhận)

Vậy x = -7; x = 5

--------

√(5x + 1)² = 6/7

|5x - 1| = 6/7

*) Với x ≥ 1/5, ta có:

5x - 1 = 6/7

5x = 6/7 + 1

5x = 13/7

x = 13/7 : 5

x = 13/35 (nhận)

*) Với x < 1/5, ta có:

5x - 1 = -6/7

5x = -6/7 + 1

5x = 1/7

x = 1/7 : 5

x = 1/35 (nhận)

Vậy x = 1/35; x = 13/35

a) (x+1)/2=(x-1)/3

=> 3(x+1)=2(x-1)

<=>3x+3=2x-2

<=>x=-5

b) (x+2)/2=8/(x+2)

=>(x+2)^2=16

=> x+2=4 hoặc x+2=-4

=> x=2 hoặc x=-6

Vậy x\(\in\){2;-6}

\(\dfrac{x+1}{2}\) = \(\dfrac{x-1}{3}\)

3.(\(x\) + 1) = (\(x\) - 1).\(2\) 

3\(x\) + 3    = 2\(x\) - 2

3\(x\) - 2\(x\)  = -3 - 2

      \(x\)     = - 5

\(\dfrac{x+2}{2}\) = \(\dfrac{8}{x+2}\)

(\(x\) + 2)² = 8.2

(\(x\) + 2)² = 16

\(\left[{}\begin{matrix}x+2=-4\\x+2=4\end{matrix}\right.\)

\(\left[{}\begin{matrix}x=-6\\x=2\end{matrix}\right.\)

a) Xét △ABE và △MBE:

BA=BM(gt)

BE: Cạnh chung

AE=ME (gt)

=> △ABE=△MBE (c.c.c)

b) Xét △ABK và △MBK:

BK:Cạnh chung

BA=BM(gt)

Góc ABK=góc MBK (△ABE=△MBE)

=> △ABK=△MBK (c.g.c)

=> Góc BAK=góc BMK=90^o 

=> KM vuông góc với BC

A=2 

C=4

Lời giải:
Theo đề ra ta có:

$xz=a; zy=b; yx=a$

t là số nào trong này hả bạn?

vẽ  cho mình thêm hình nhé