Phân tích đa thức thành nhân tử thôi bạn :

Ta có :

\(h\left(x\right)=x^2+5x+6\)

\(h\left(x\right)=x\left(x+2\right)+3\left(x+2\right)\)

\(h\left(x\right)=\left(x+2\right)\left(x+3\right)\)

\(\Rightarrow N_oh\left(x\right)=-2;-3\)

\(g\left(x\right)=2x^2+7x-9\)

\(g\left(x\right)=2x^2+9x-2x-9\)

\(g\left(x\right)=2x\left(x-1\right)+9\left(x-1\right)\)

\(g\left(x\right)=\left(x-1\right)\left(2x+9\right)\)

\(\Rightarrow N_og\left(x\right)=1;-4,5\)

ko biet

chiu nhe ban 

1+1/2.(1+2)+1/3.(1+2+3)+1/4.(1+2+3+4)+...+1/2023.(1+2+3+...+2023)

=1+1/2.(1+2).2/2+1/3.(1+3).3/2+1/4.(1+4).4/2+...+1/2023.(1+2+3+...+2023).2023/2

=2/2+3/2+4/2+...+2023/2

=2+3+4+...+2023/2

=2025.2022/2/2                 

=1023637,5                        

tham khảo thôi nha

Lời giải:

BĐT $\Leftrightarrow abc\geq (a+b-c)(b+c-a)(c+a-b)(*)$

Áp dụng BĐT AM-GM:

$(a+b-c)(b+c-a)\leq \left(\frac{a+b-c+b+c-a}{2}\right)^2=b^2$
$(b+c-a)(c+a-b)\leq \left(\frac{b+c-a+c+a-b}{2}\right)^2=c^2$

$(a+b-c)(a+c-b)\leq \left(\frac{a+b-c+a+c-b}{2}\right)^2=a^2$
Nhân theo vế 3 BĐT trên: 

$[(a+b-c)(b+c-a)(c+a-b)]^2\geq (abc)^2$

$\Rightarrow abc\geq (a+b-c)(b+c-a)(c+a-b)$ (BĐT $(*)$ được cm)

Ta có đpcm.

Đổi 1 giờ 30 phút = 1,5 giờ

Tỉ số gian người đi xe máy trên cả quãng đường so với thời gian người đi xe đạp trên cả quãng đường là:

                     1 : 3 = \(\dfrac{1}{3}\)

Theo bài ra ta có sơ đồ:

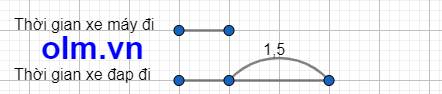
Theo sơ đồ ta có:

Thời gian người đó đi xe đạp trên cả quãng đường AB là:

                           1,5 : ( 3 - 1) \(\times\) 3 = 2,25 giờ

Vận tốc của xe đạp khi đi trên quãng đường AB là:

                              36 : 2,25 = 16 (km/h)

Vận tốc của xe máy là: 16 \(\times\) 3 = 48 (km/h)

Đáp số: vận tốc xe máy 48 km/h

                vận tốc xe đạp 16 km/h